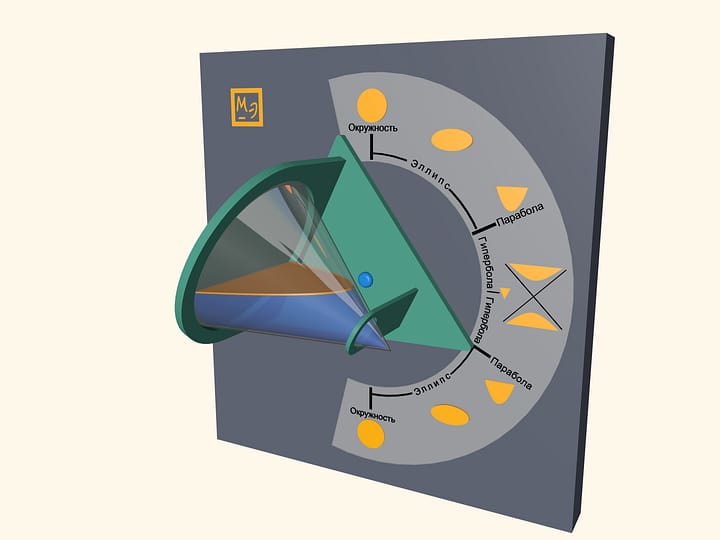
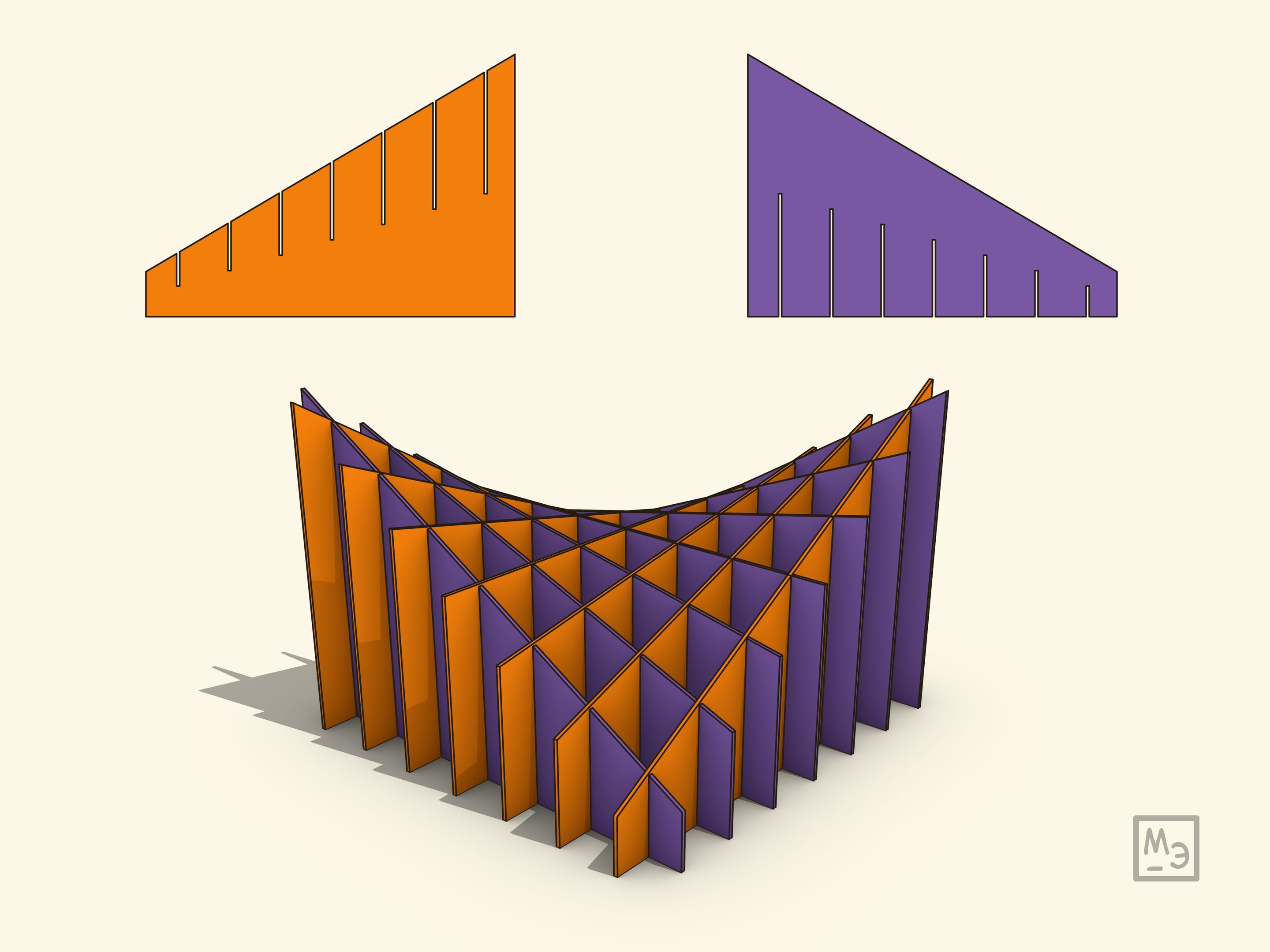
The cardboard model of the hyperbolic paraboloid is amazing. Its name includes words that are only studied in high school (separately, but together only at university). It allows one to see clearly the non-trivial properties of this complex surface. It is also possible to make and discuss such a model even with children.
One can see an animated definition of the hyperbolic paraboloid and understand where there are parabolas and where there are hyperbolas by watching the film Saddle surface: hyperbolic paraboloid. And the property of the linearity of this saddle surface — that it is formed by the motion of a straight line — can be demonstrated by doing the counterintuitive chip experiment shown in Chips: hyperbolic paraboloid.
The cardboard model allows one to see even more clearly the linearity property of the hyperbolic paraboloid — it explicitly presents generatrix from both families. Again clearly the cardboard model also allows to make sure that the surface of the hyperbolic paraboloid is “not flat” (has negative Gaussian curvature) — a piece of paper cannot be placed on it without crumpling.
The model of hyperbolic paraboloid under consideration is bendable: it can be shrunk by keeping the pieces of paper parallel in each of the two families, but by changing the angle between these families. The intersection points of the formations will obviously remain unchanged, the surface itself will change, but will always remain a hyperbolic paraboloid. The right angle case corresponds to the “school” rectangular hyperbolas when their asymptotes are perpendicular. Theoretically, you could make such a panorama book (Pop Up), but if you use unbendable (respectively, relatively thick) cardboard, the number of layers is too high for it to close “flat” well.