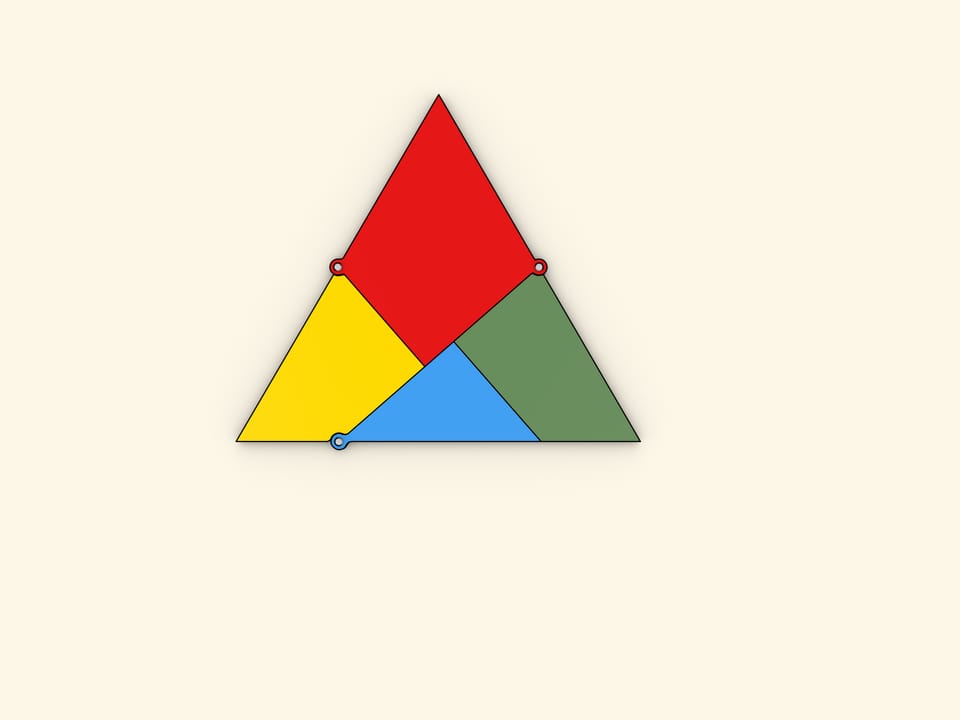
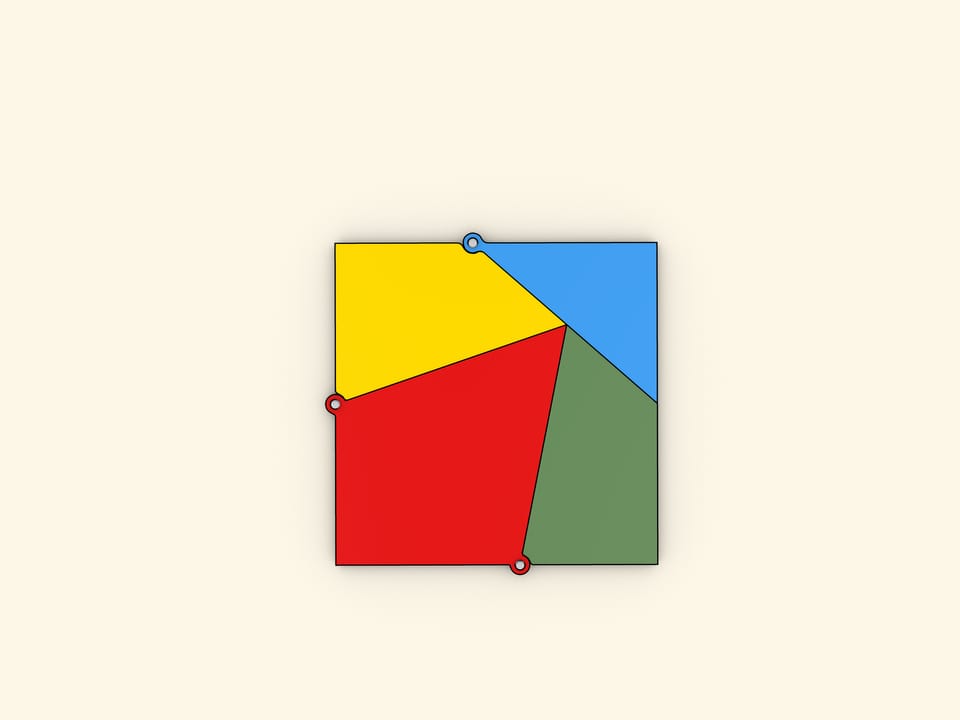
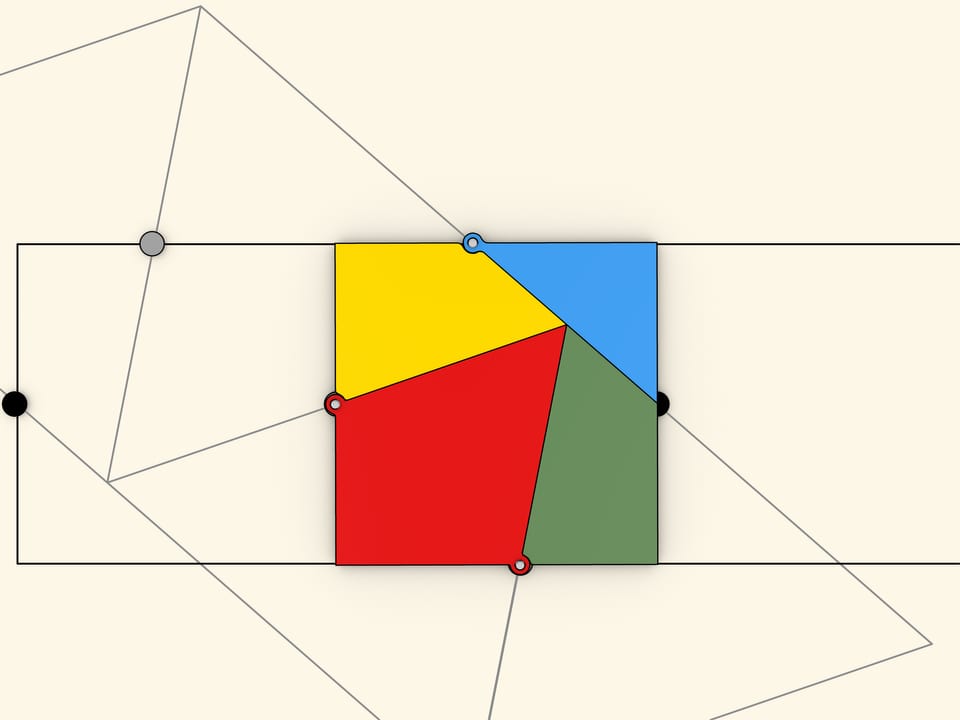
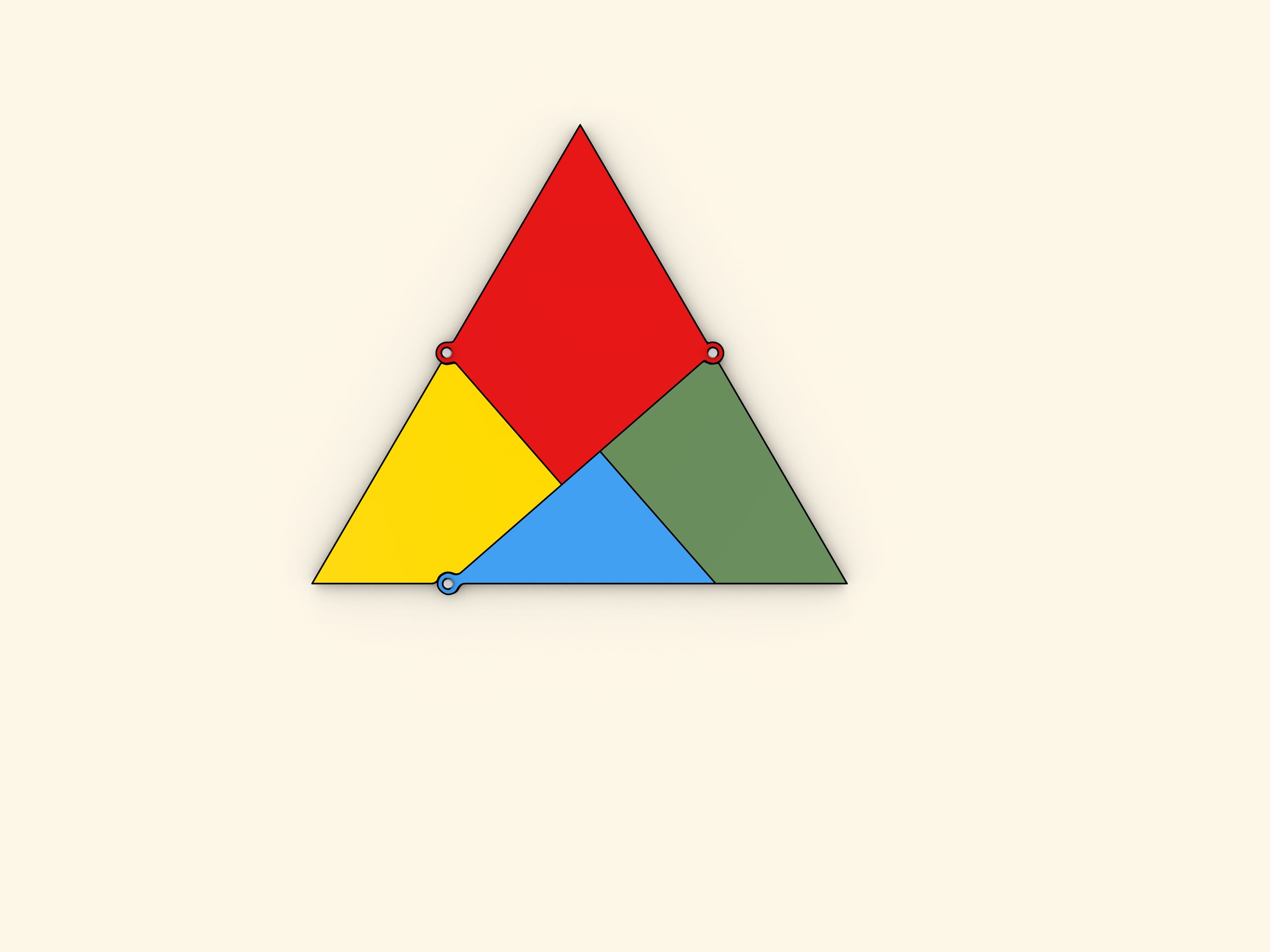
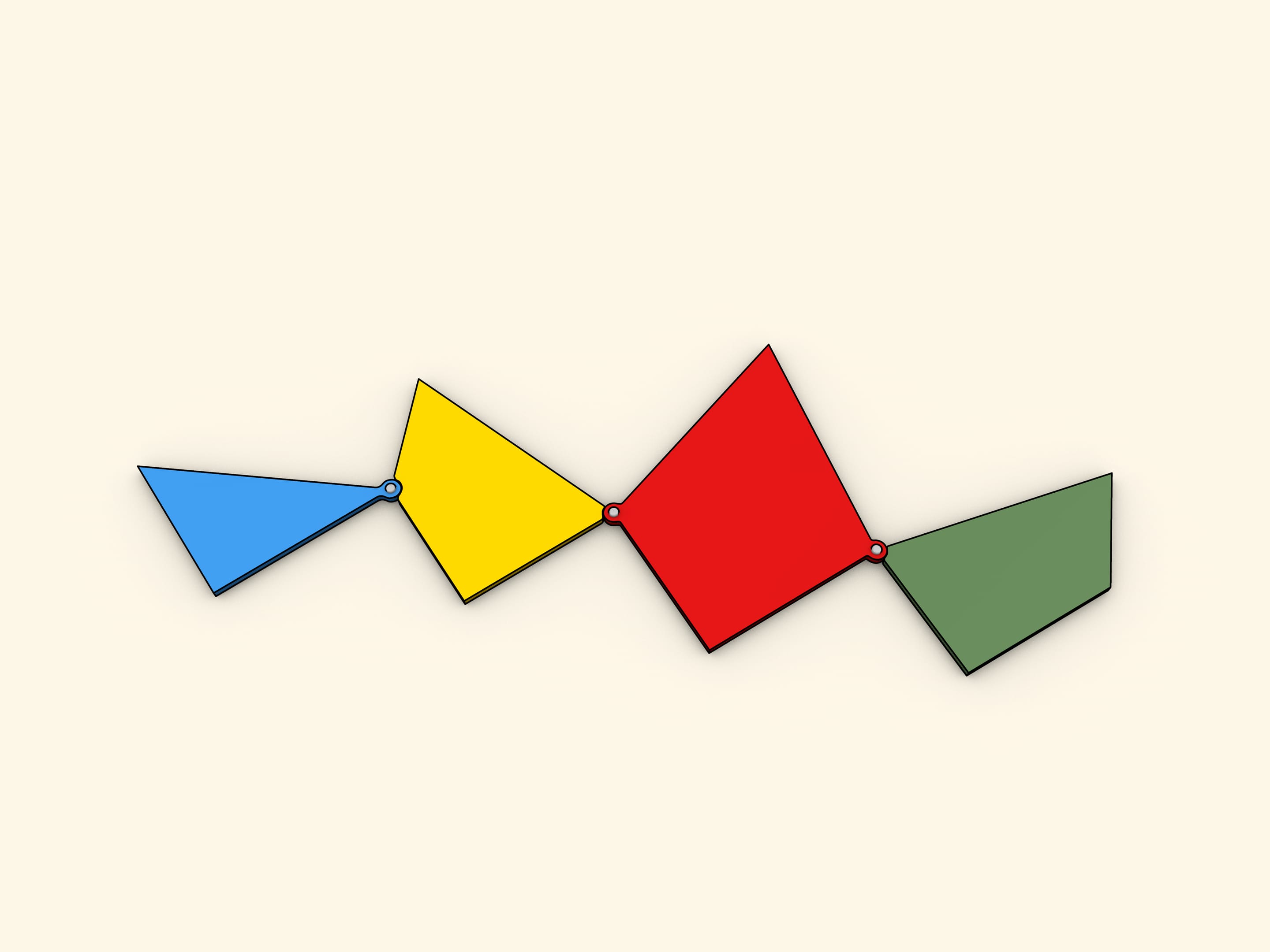
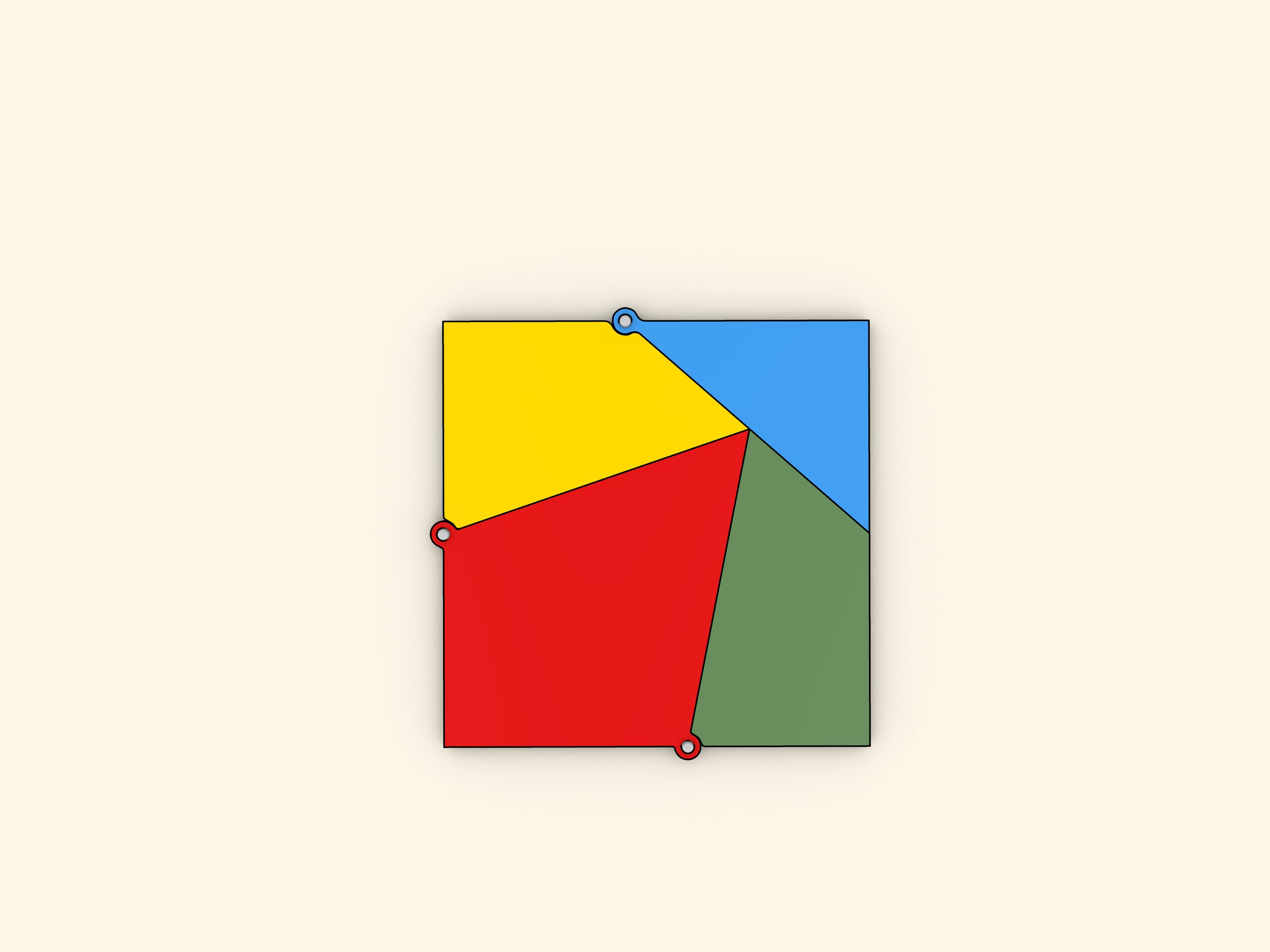
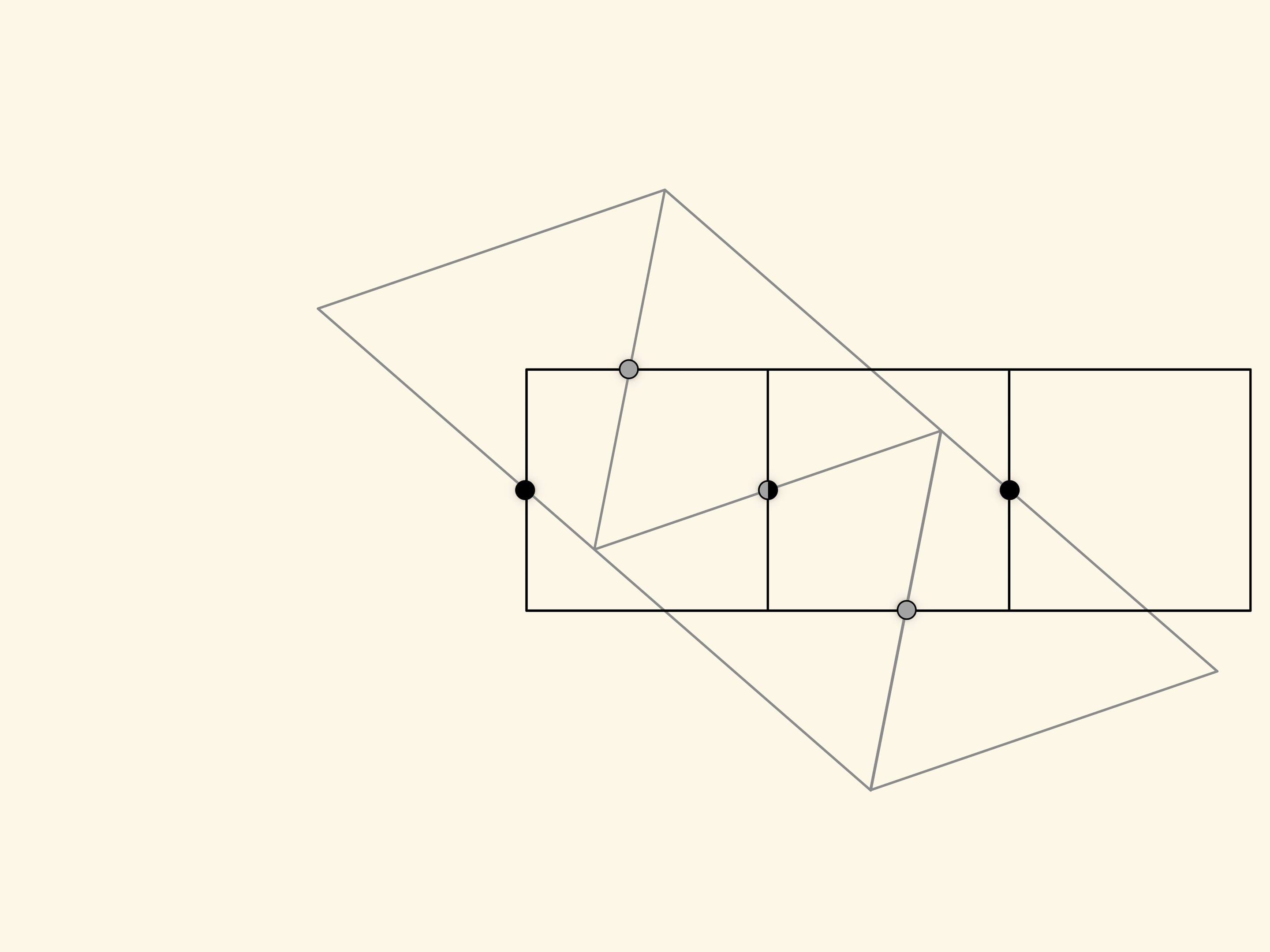
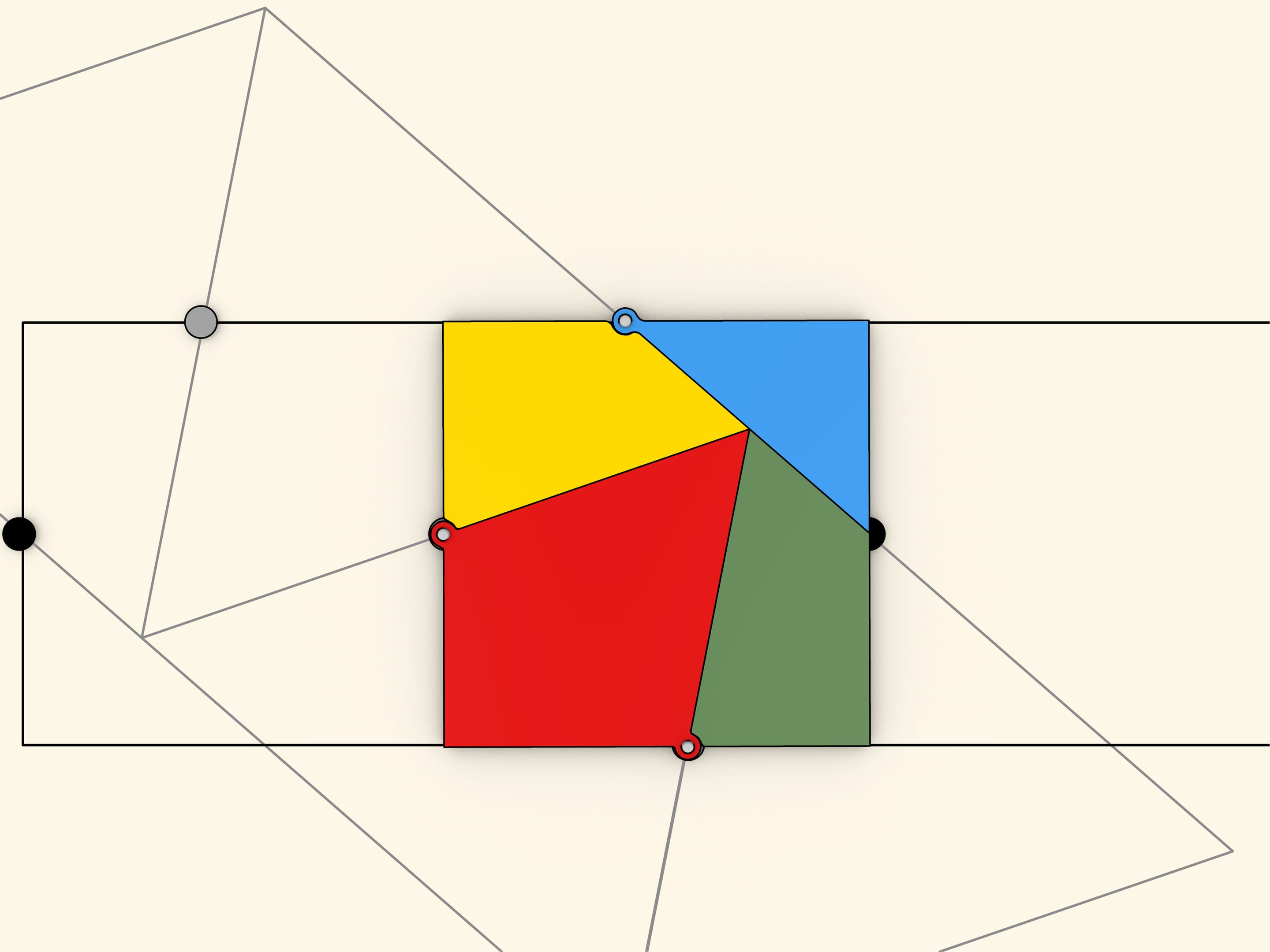
What is the minimal number of parts an equilateral triangle should be cut into so that a square can be formed rearranging them? This problem was offered as a challenge to the readers of the Daily Mail newspaper issued as of 1st and 8th February 1905. Among hundreds answers obtained, only one was right: four parts are enough.
Dudeney writes:
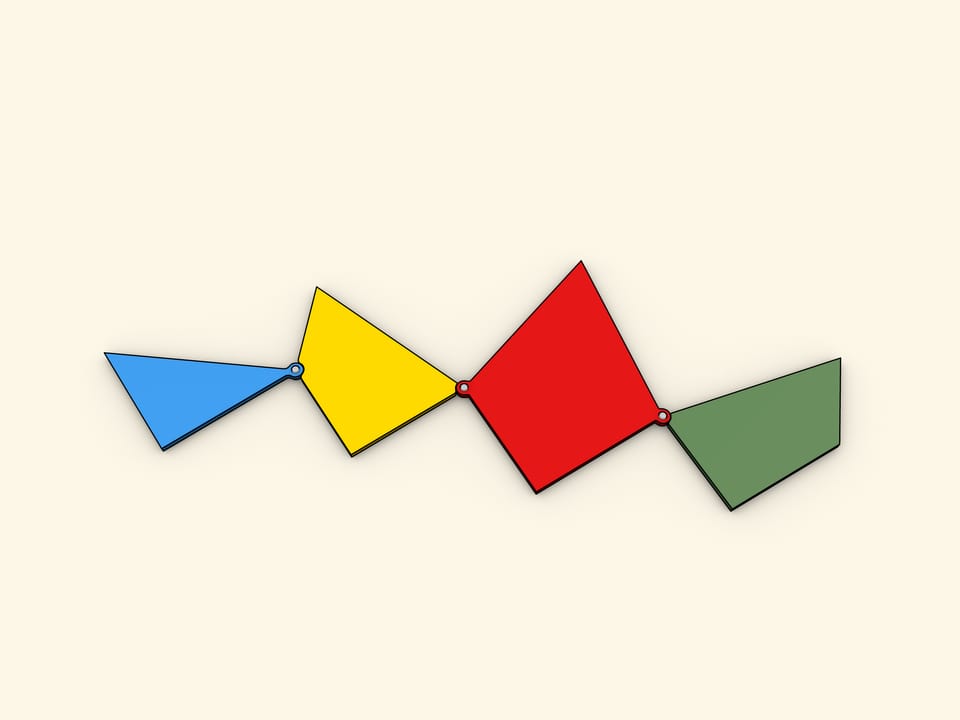
I add an illustration showing the puzzle in a rather curious practical form, as it was made in polished mahogany with brass hinges for use by certain audiences.
It will be seen that the four pieces form a sort of chain, and that when they are closed up in one direction they form the triangle, and when closed in the other
direction they form the square.
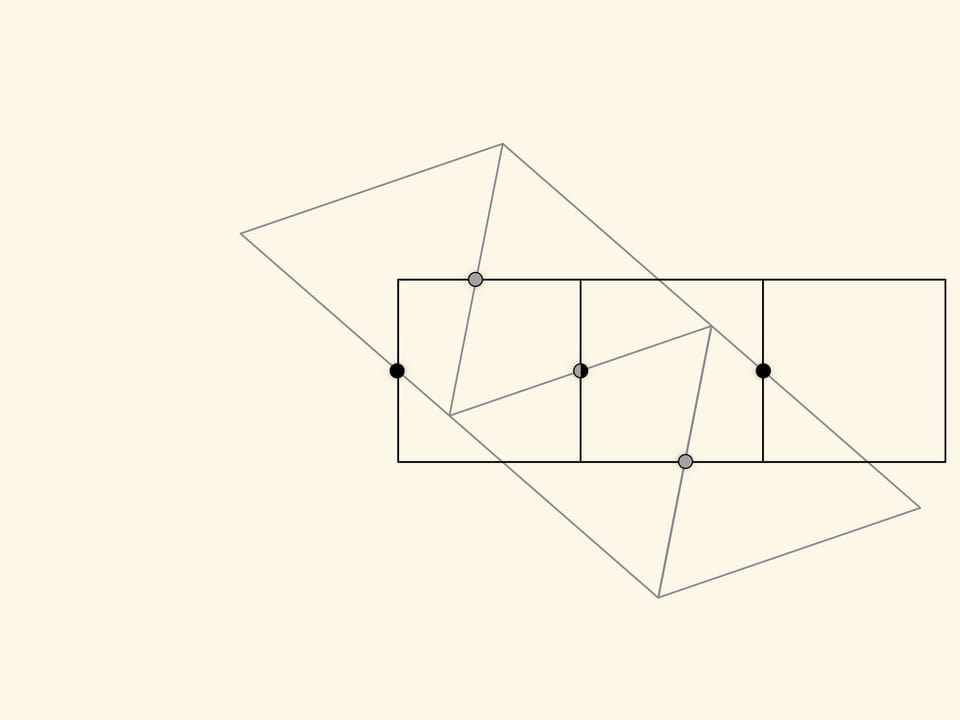
How can one guess such a dissection? Take a triangle and a square of equal area and make two regular stripes, repeating each of the shapes. Putting the stripes above one another so that the maximum number of one's side midpoints matches the sides of the other, the desired dissection is obtained. This is in a way a general method of finding dissections of equal area polygons. Solving such problems is the subject of Harry Lindgren's ”Recreational problems in geometric dissections and how to solve them” book.