The number of degrees of freedom (DOF) is a number of independent parameters that unambiguously define the state of a mechanical system.
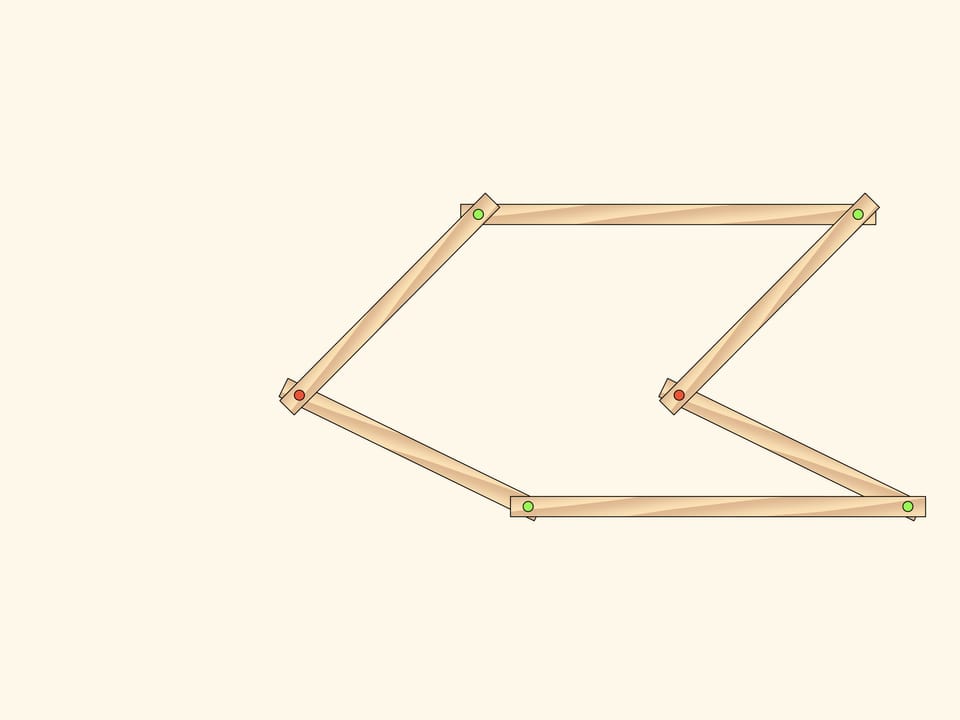
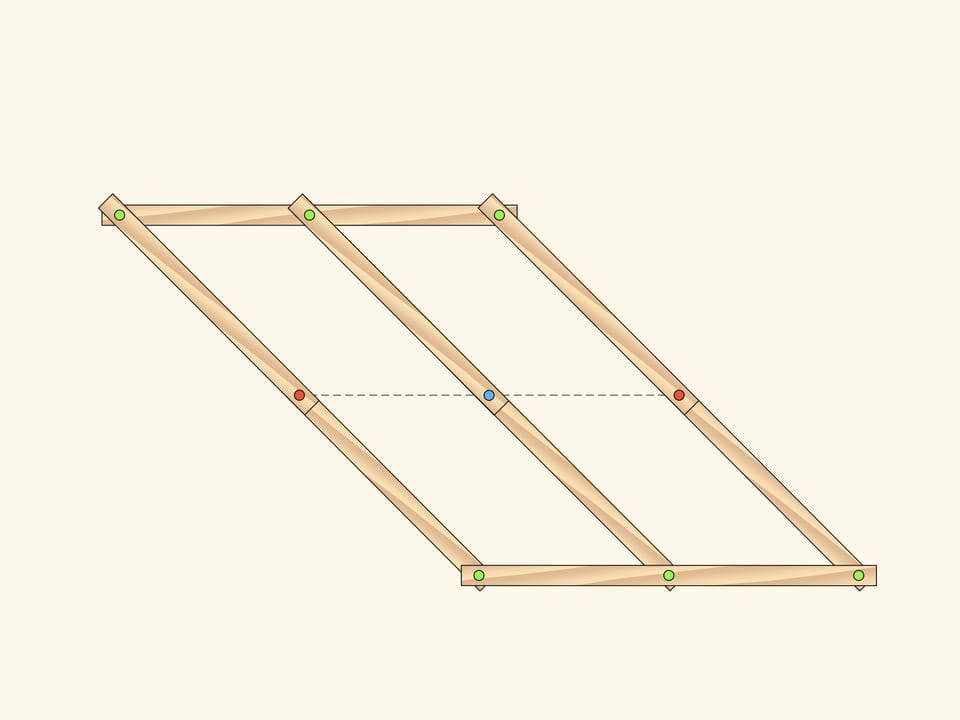
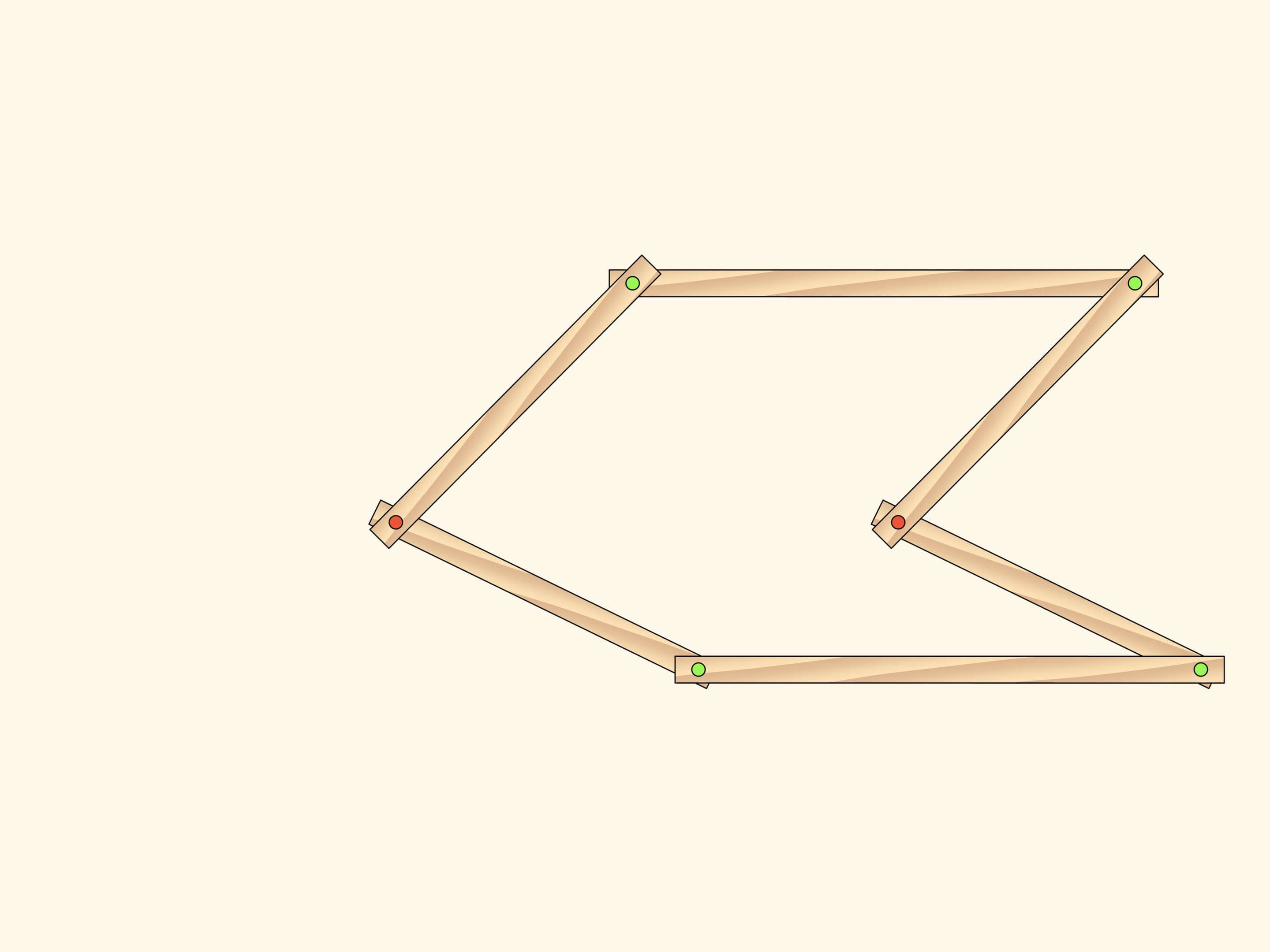
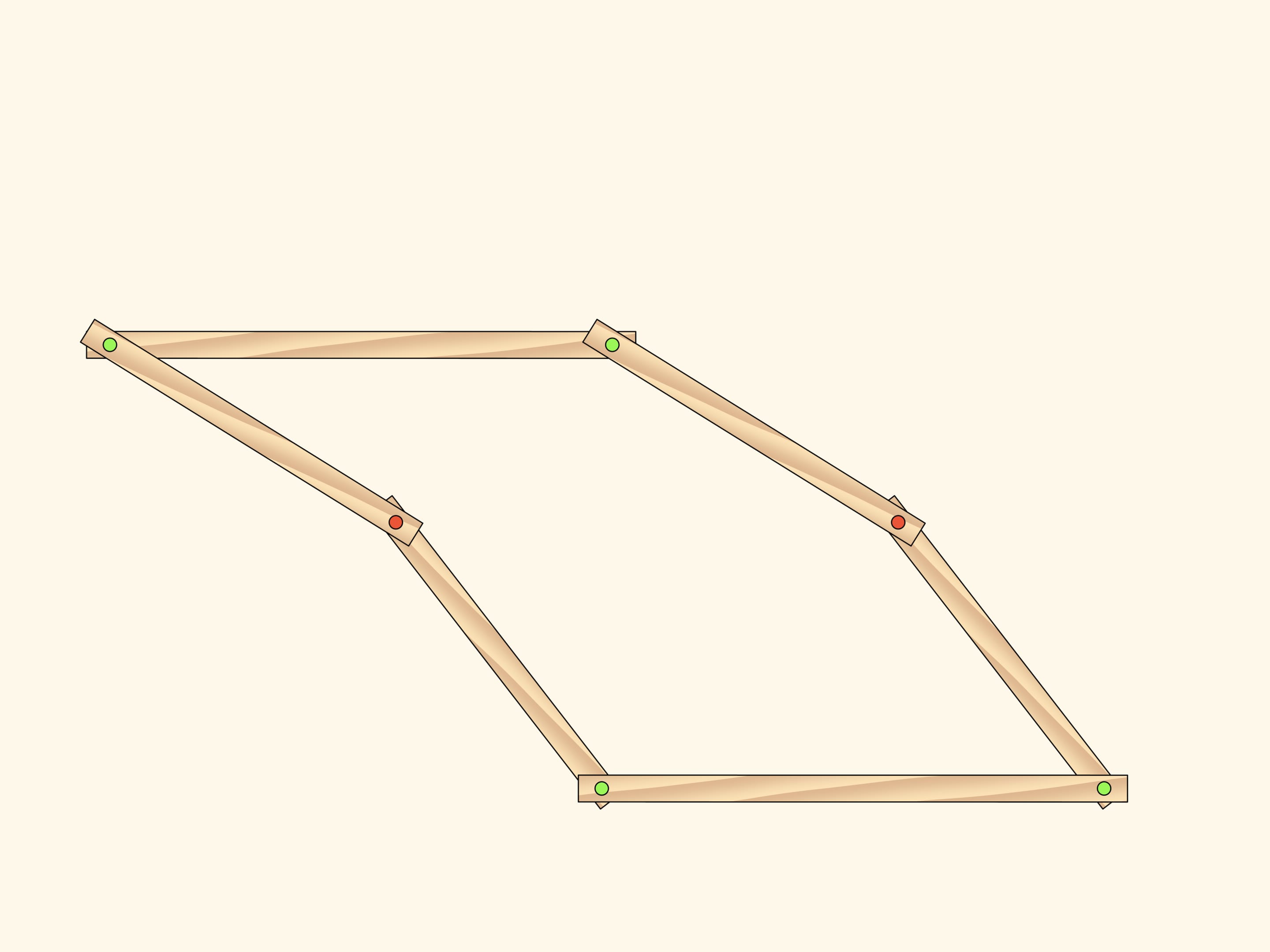
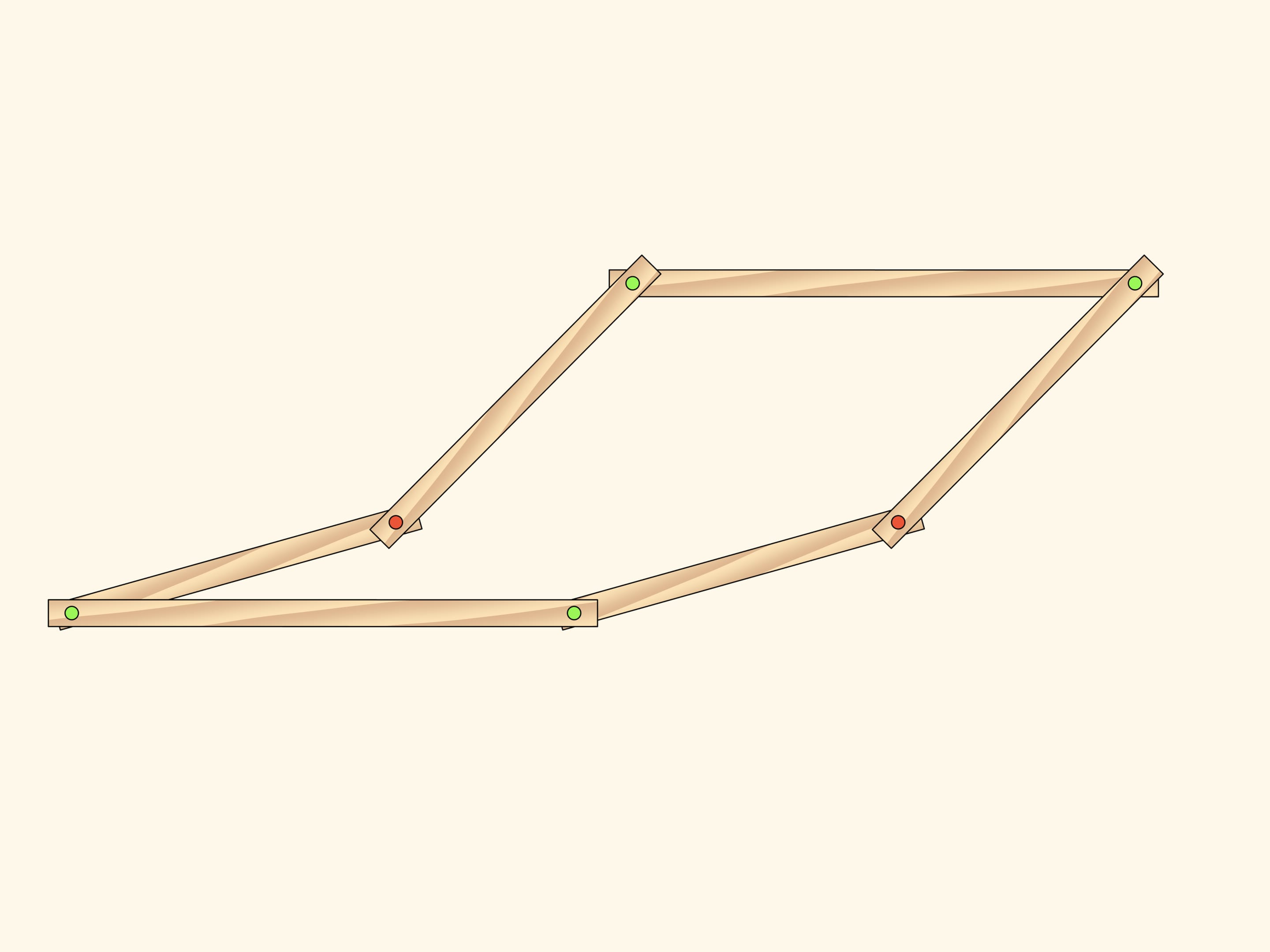
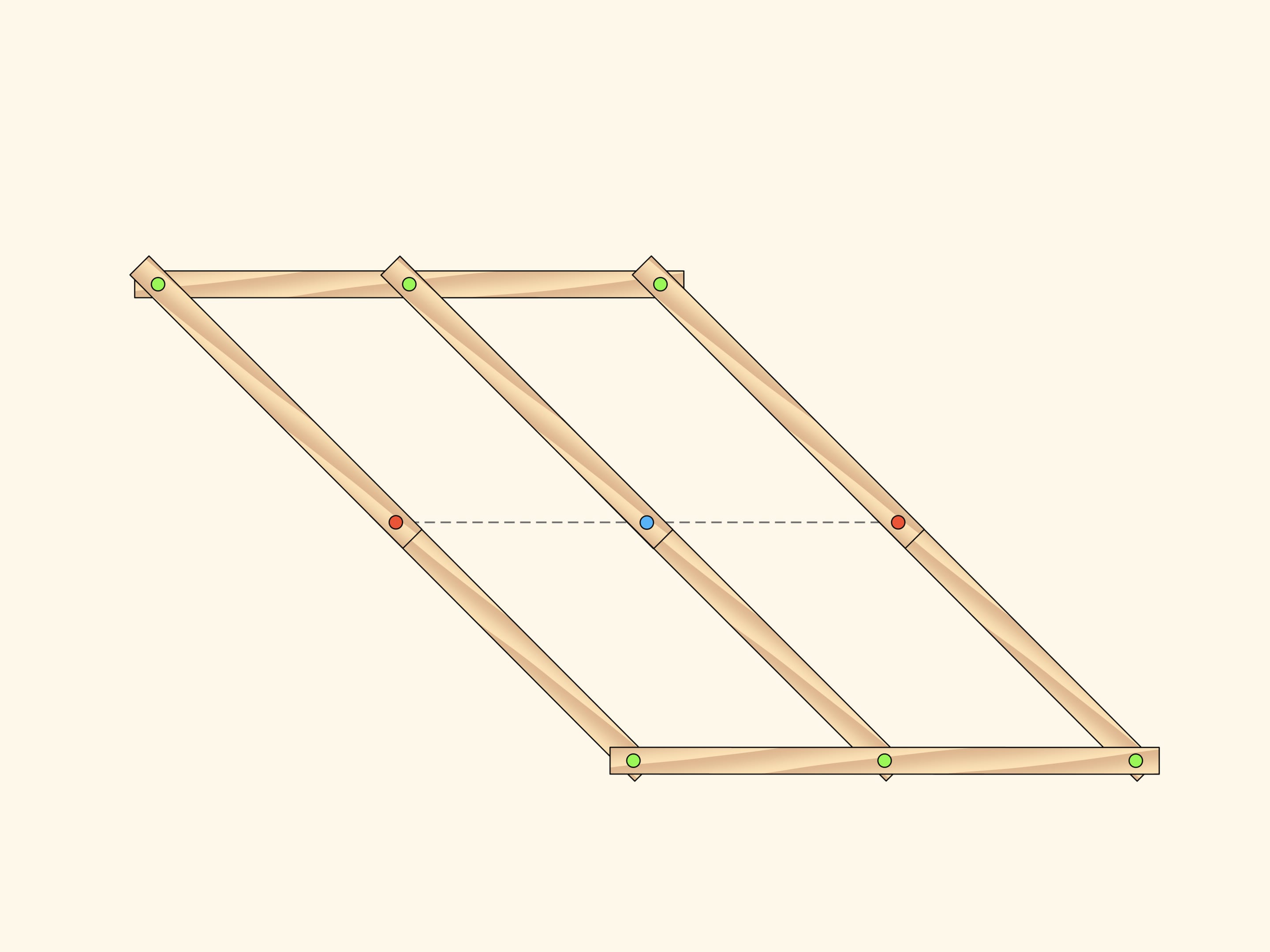
Consider a plane hinge mechanism ñconsisting of two similar parallelograms that have two common fixed red hinges. The number of DOF of such a mechanism obviously equals two as parallelograms can rotate independently and as parameters one may take, for example, the angles counted off the horizontal direction.
Does every mechanism has a number of DOF «fixed»? Or there are mechanisms whose number of DOF is variable? It turns out that there are…
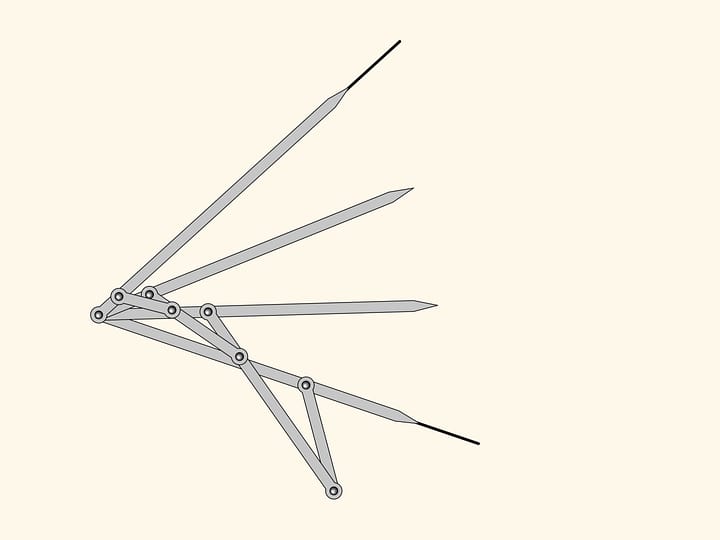
The plane first hinge mechanism with a variable number of DOF was invented by W. Wunderlich in 1954. It contained two fixed hinges and 12 edges. We'll consider a simpler construction with 9 edges created by a russian mathematician Michael Kovalev.
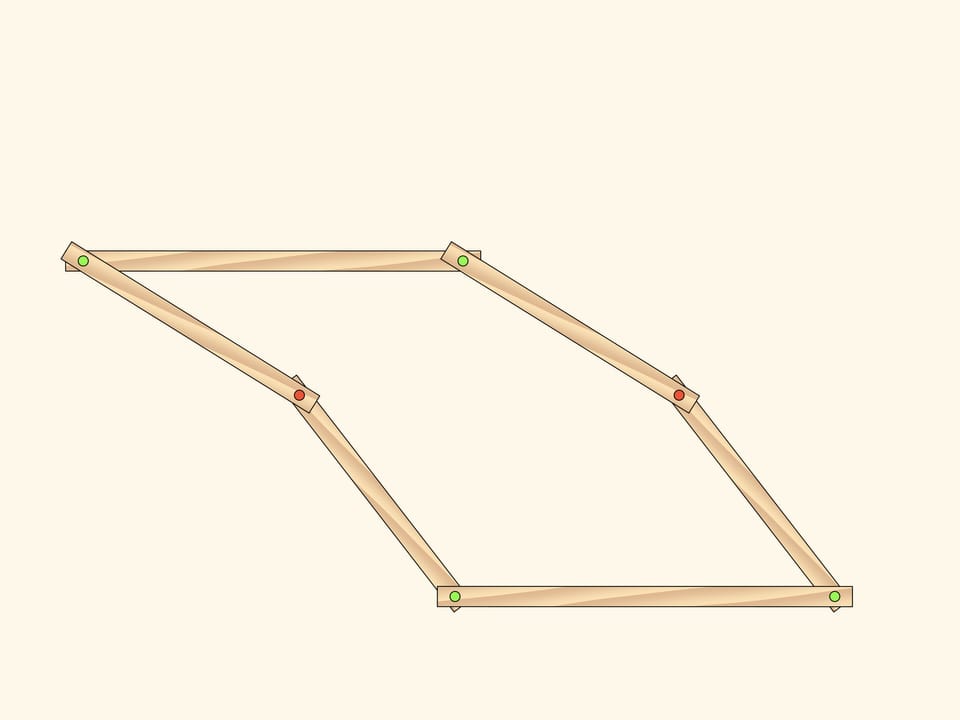
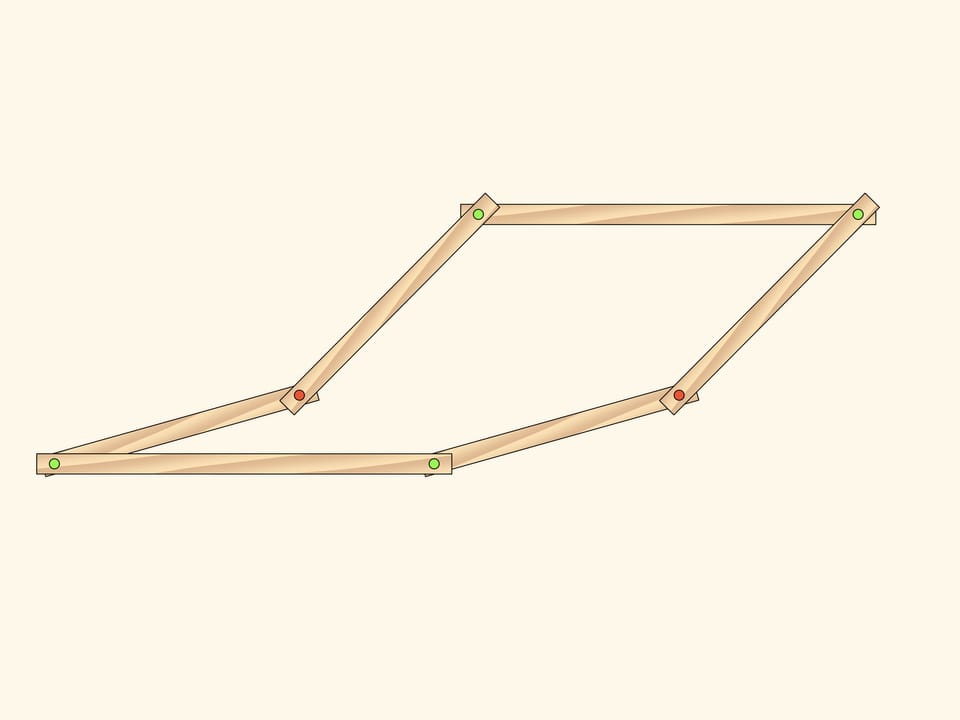
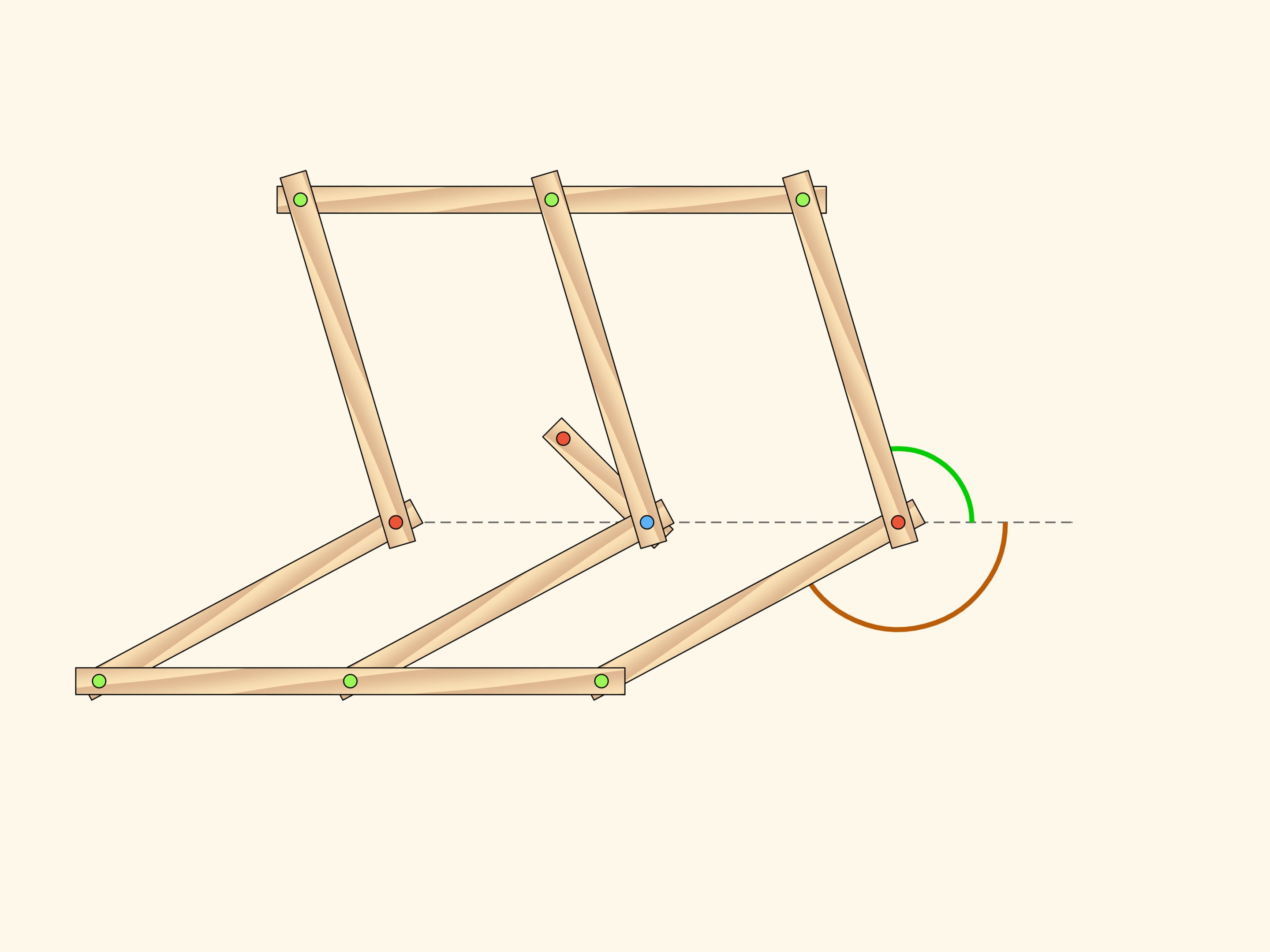
Addto the parallelograms «centerlines» and a short edge connecting their intersection point with a fixed red hinge.
While the blue hinge remains on the central line that connects two initial fixed red hinges, the additional edges don't change the number of DOF. The state is defined, for example, by two rotation angles counted off the horizontal direction.
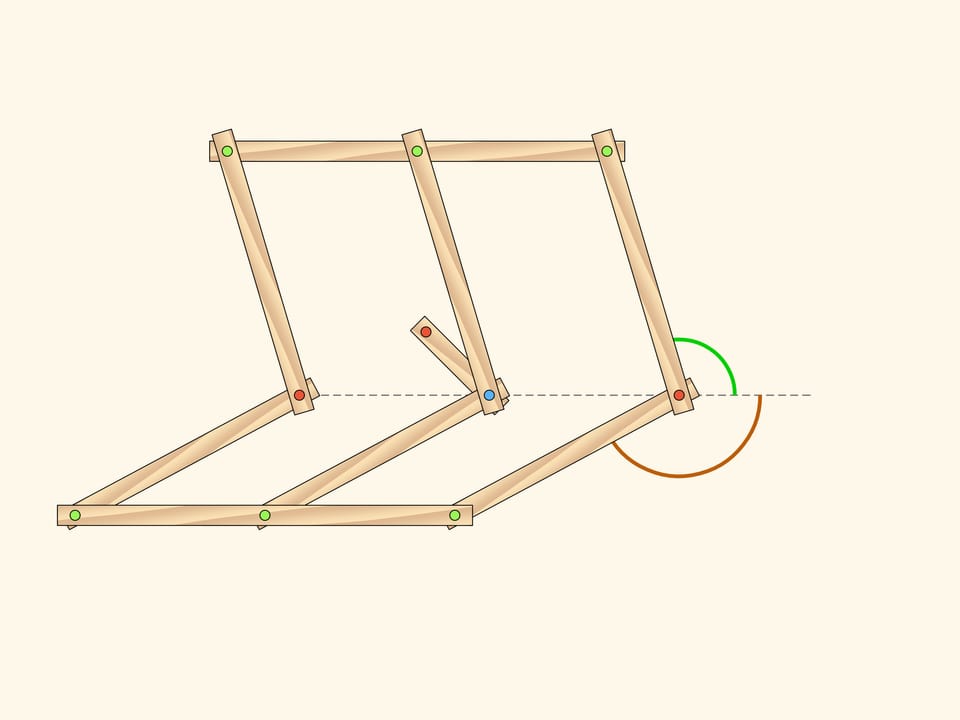
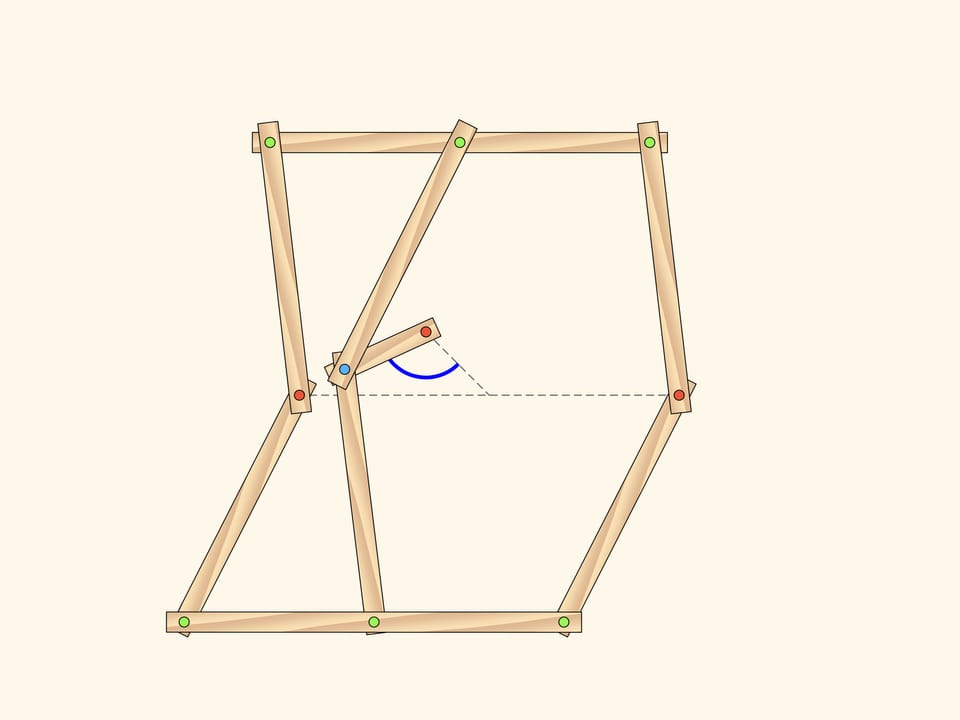
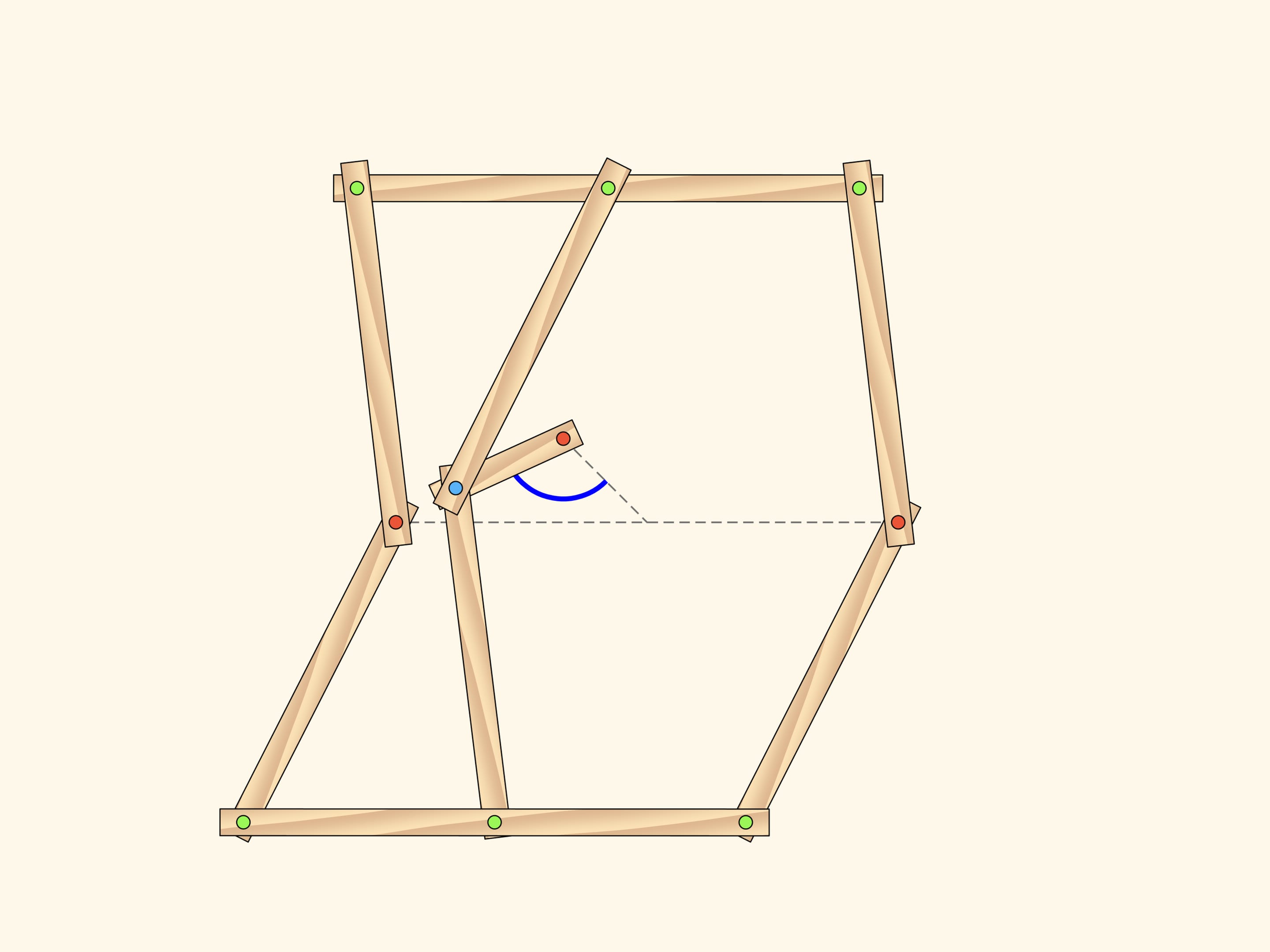
However, the blue hinge may leave the central line when the centerlines and the short edge lie on the same line. As soon as the blue hinge is off the central line, the state of the whole mechanism is defined by a single parameter! This parameter can be, for example, the angle between the initial and the current location of the short edge.