Since James Watt invented the steam engine there was a problem of transforming rotary motion of one hinge into perfect straight-line motion of another. Thus, a straight-line mechanism.
During a long time scientists and engineers couldn't solve this problem, were constructing approximate solutions drawing not perfect straight lines. And only beautiful mathematics helped finally to solve this problem.
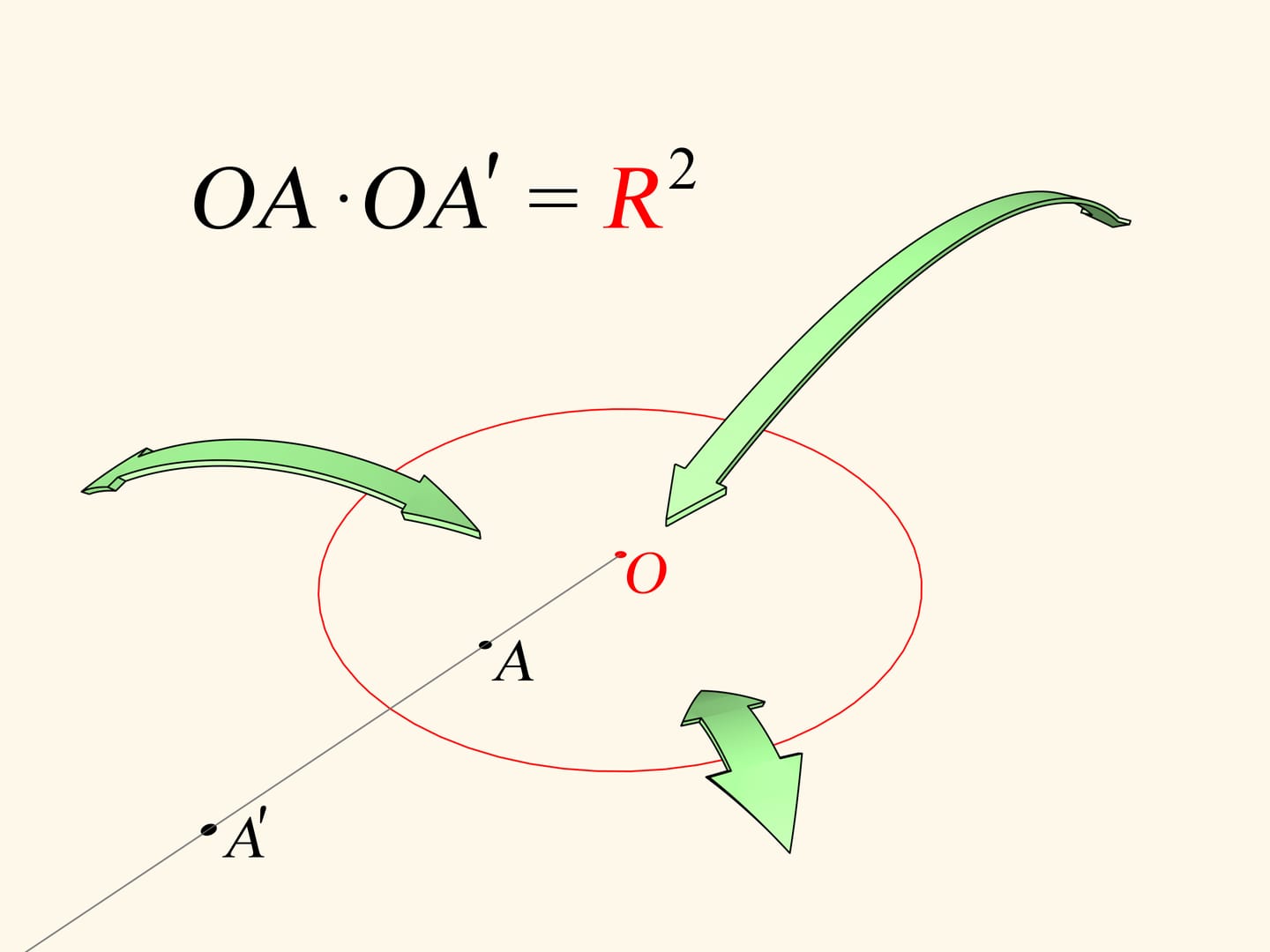
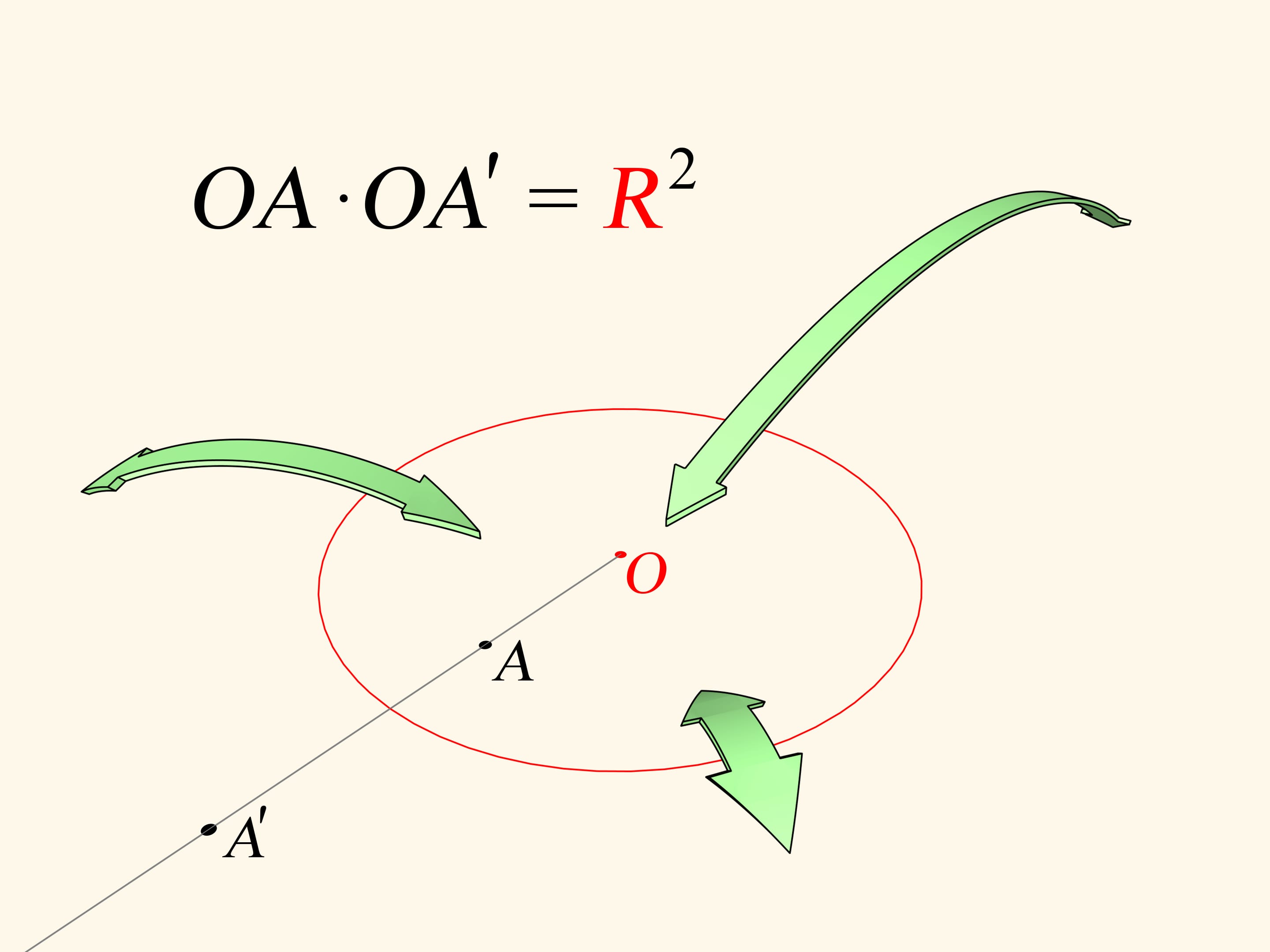
Let's recall that plane circle inversion is a bijective mapping of the inner part of the circle (except a single point, the center) onto the outer part. The image of the point $A$ is the point $A’$ lying on the ray starting at the center and passing through $A$. Its position is determined by the equality $OA \cdot OA'=R^2$. Inversion helps to solve many interesting problems in geometry. As we'll se, it helps not only in theoretical questions.
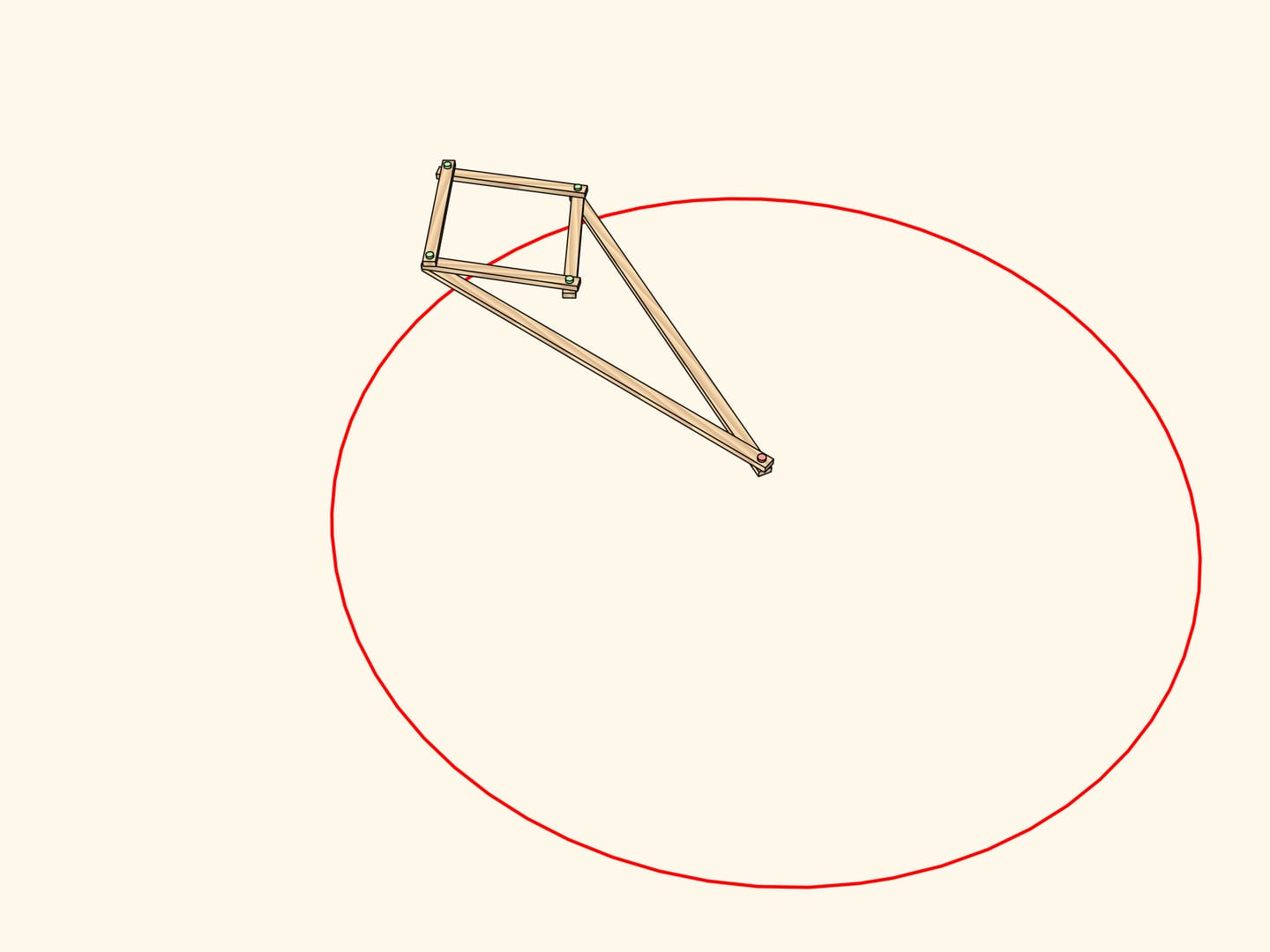
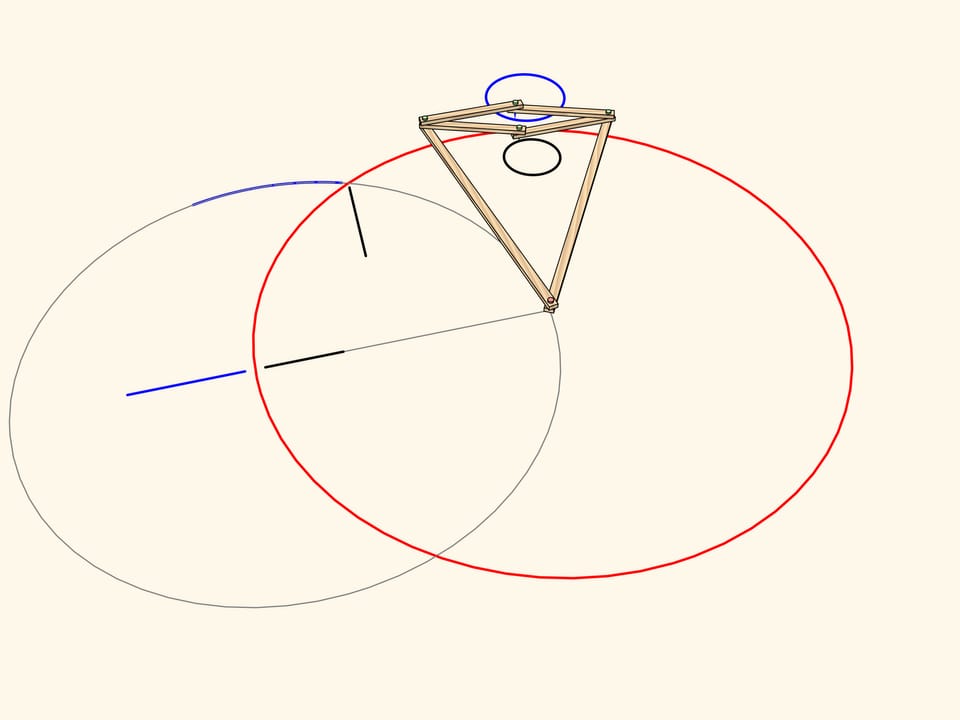
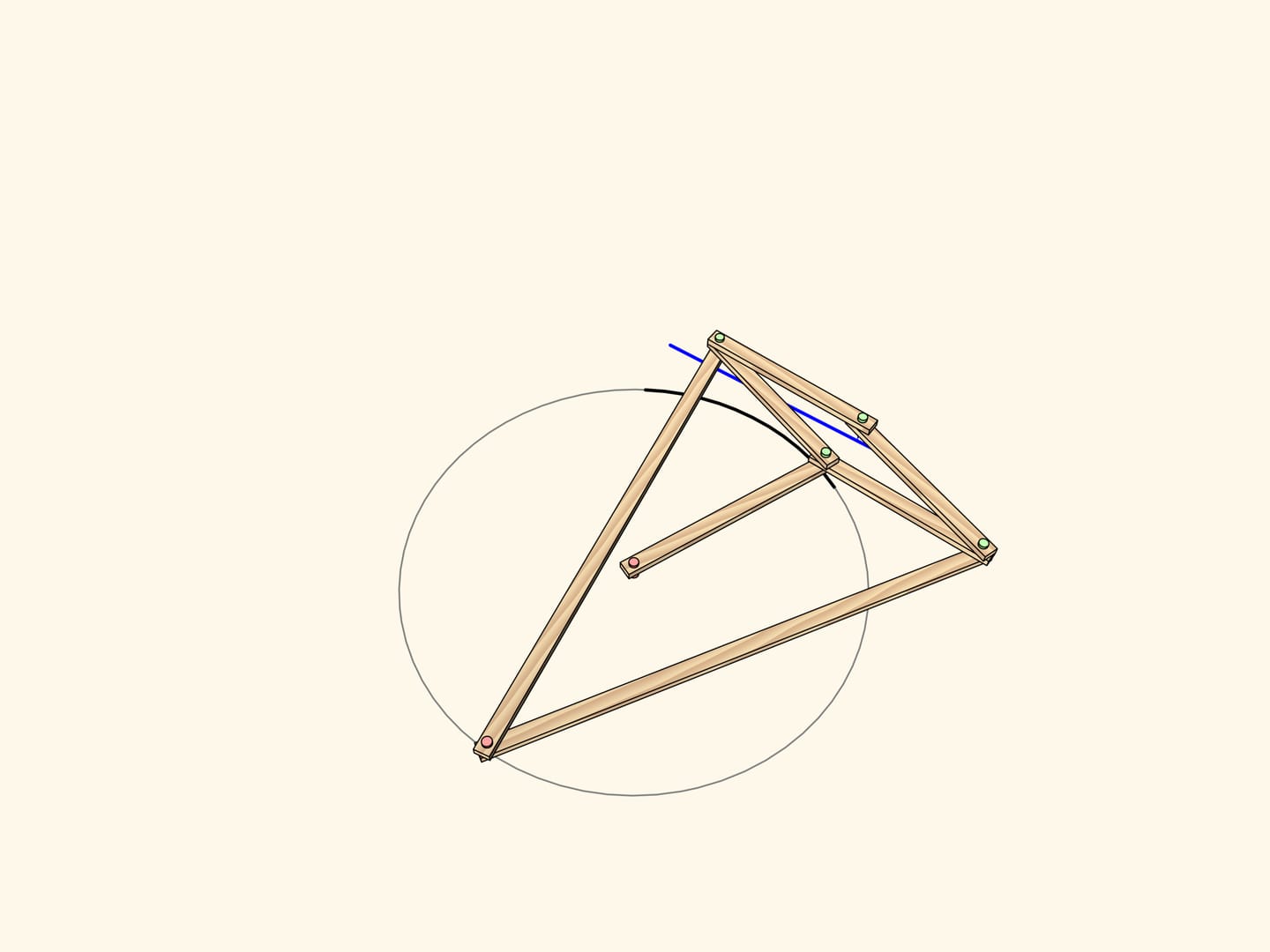
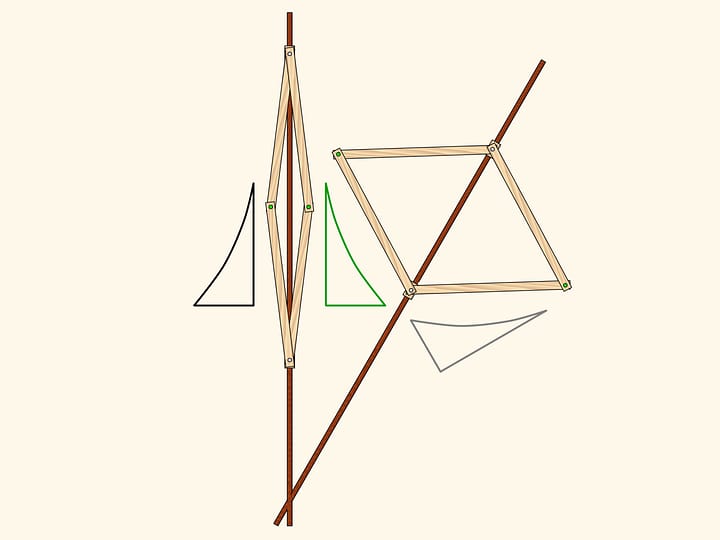
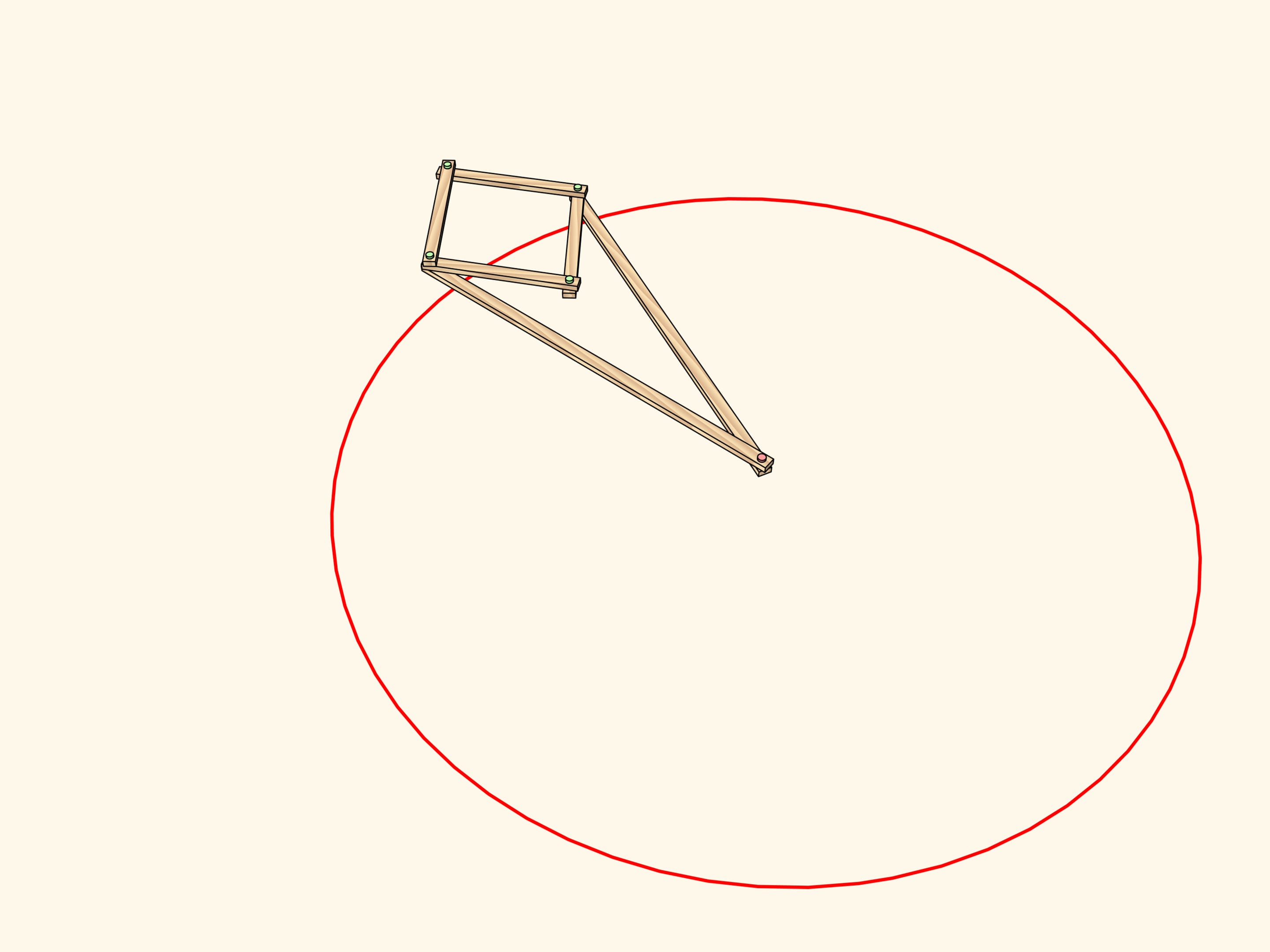
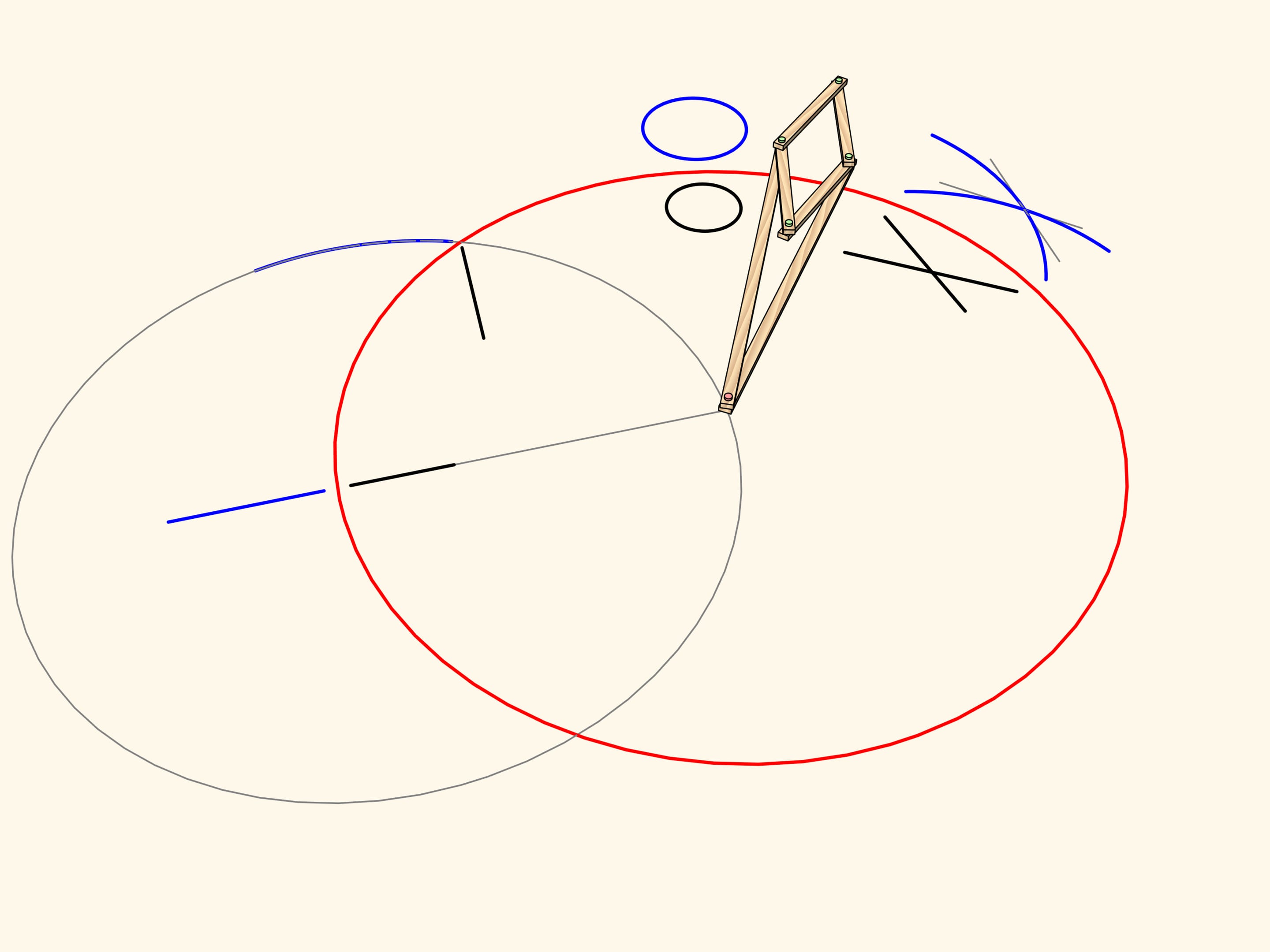
Consider a linkage with one fixed red hinge. The ends of two equal edges are attached to a hinged rhomb.
This mechanism implements inversion with respect to a circle centered in the fixed hinge and radius depending on the edge lengths.
Let's see using our mechanism what properties inversion has.
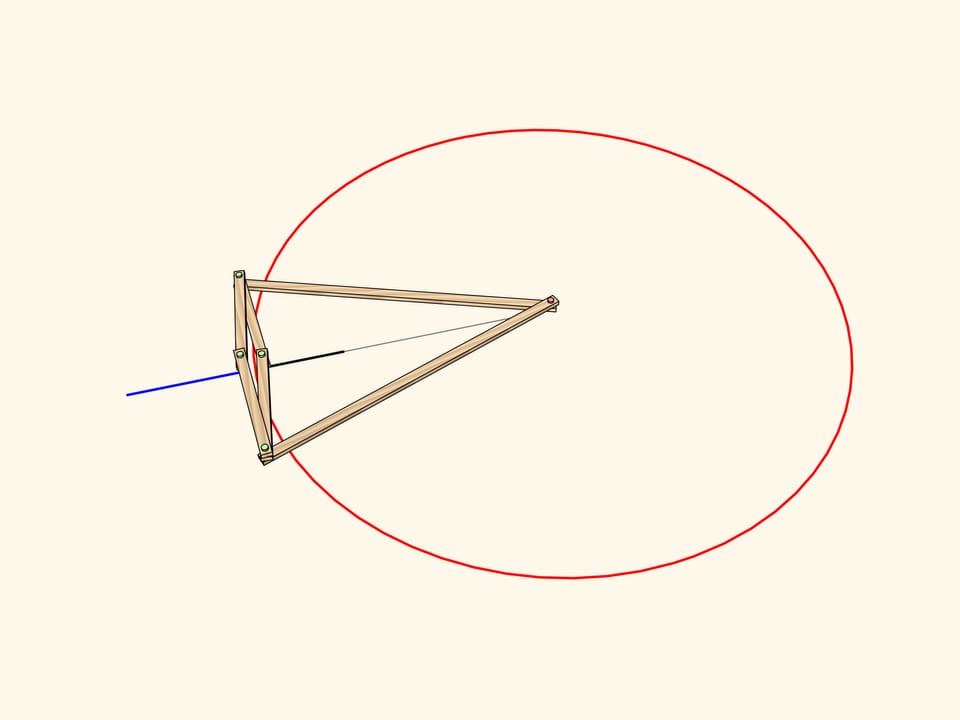
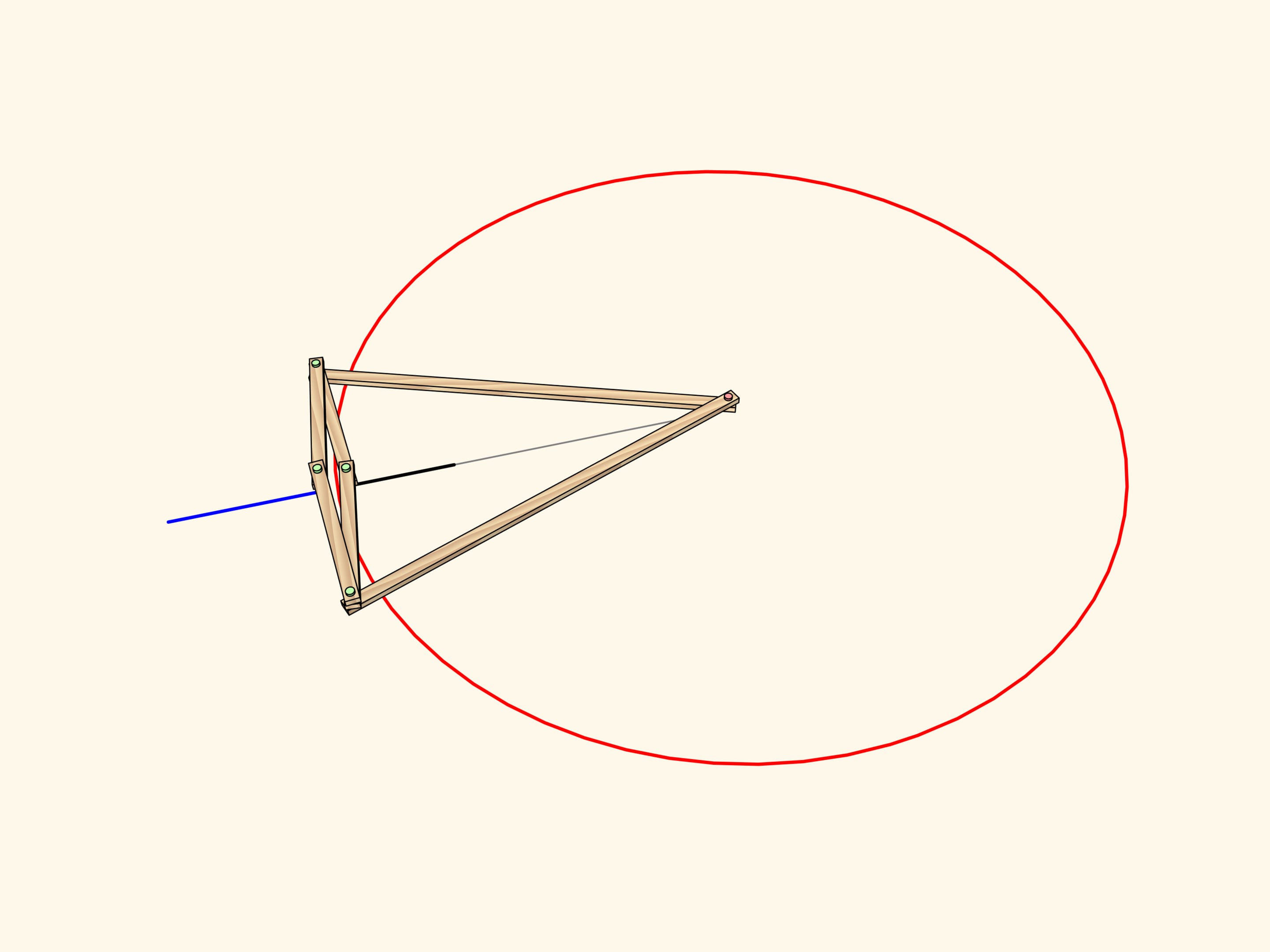
From the definition of inversion it is clear that the image of a segment of a line passing through the center is mapped again to a segment lying on the same line.
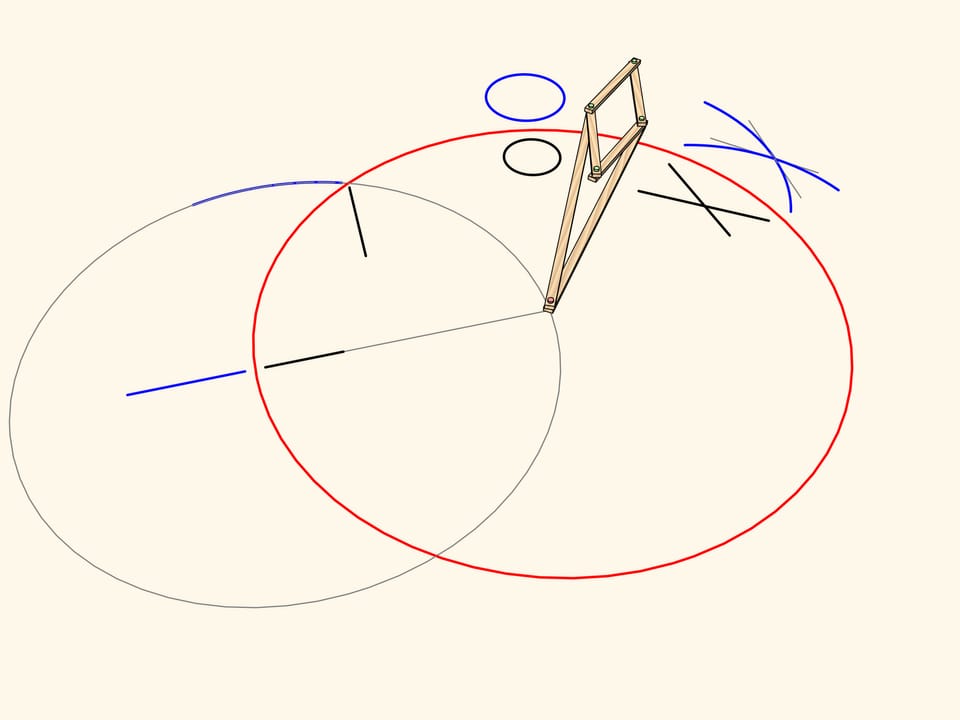
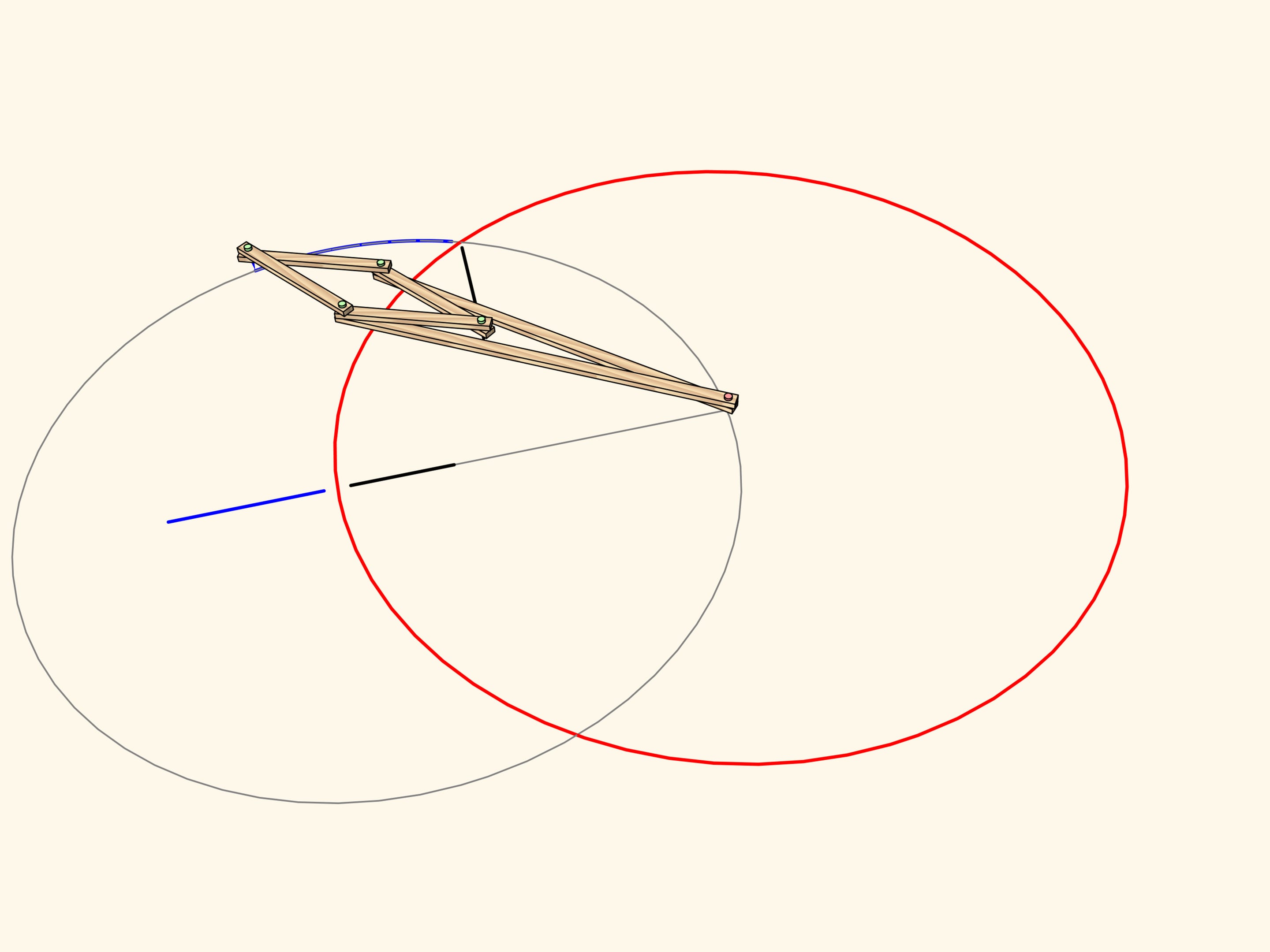
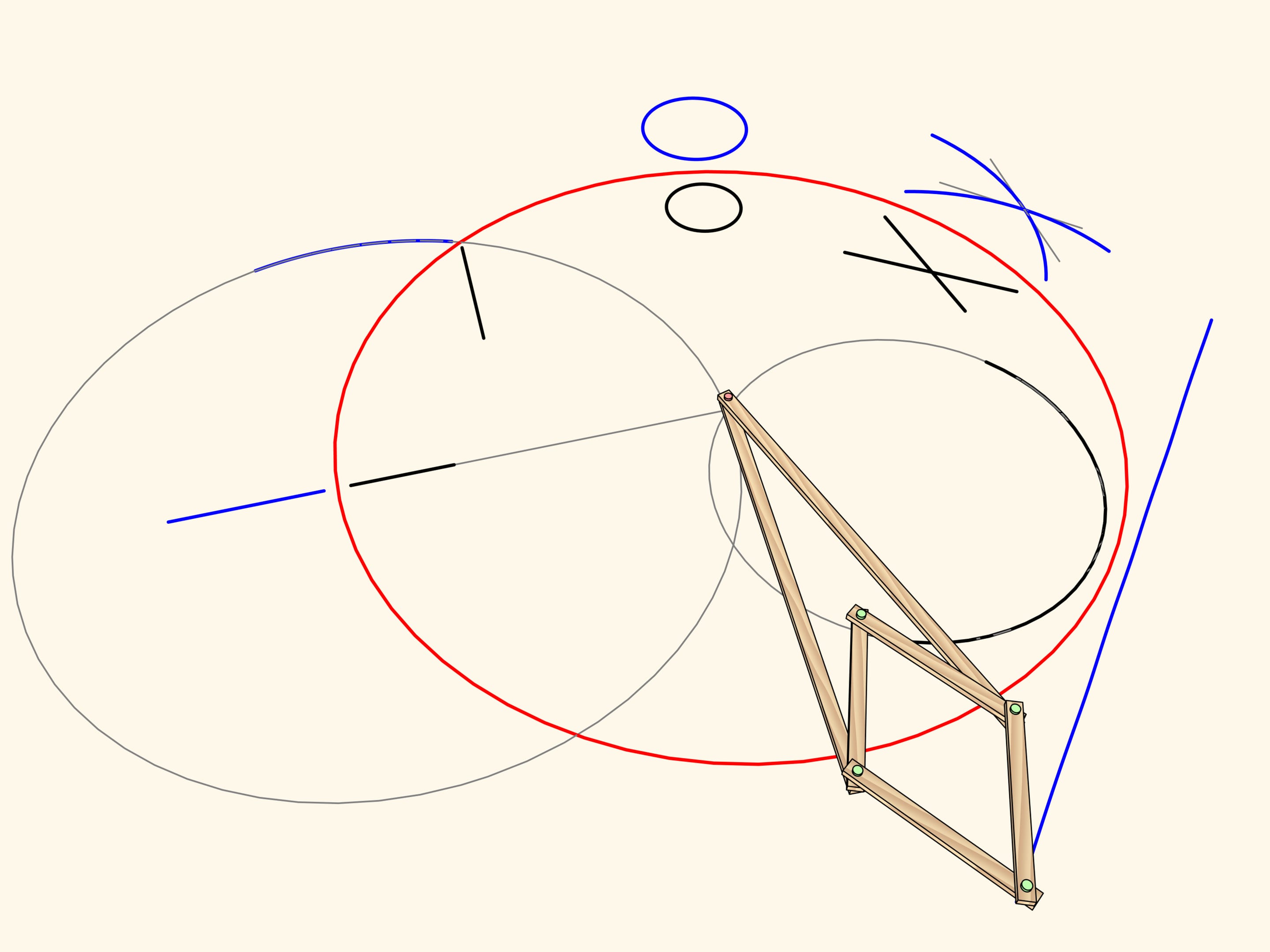
The image of a segment of a line not passing through the center is an arc of a circle, passing through the center of inversion.
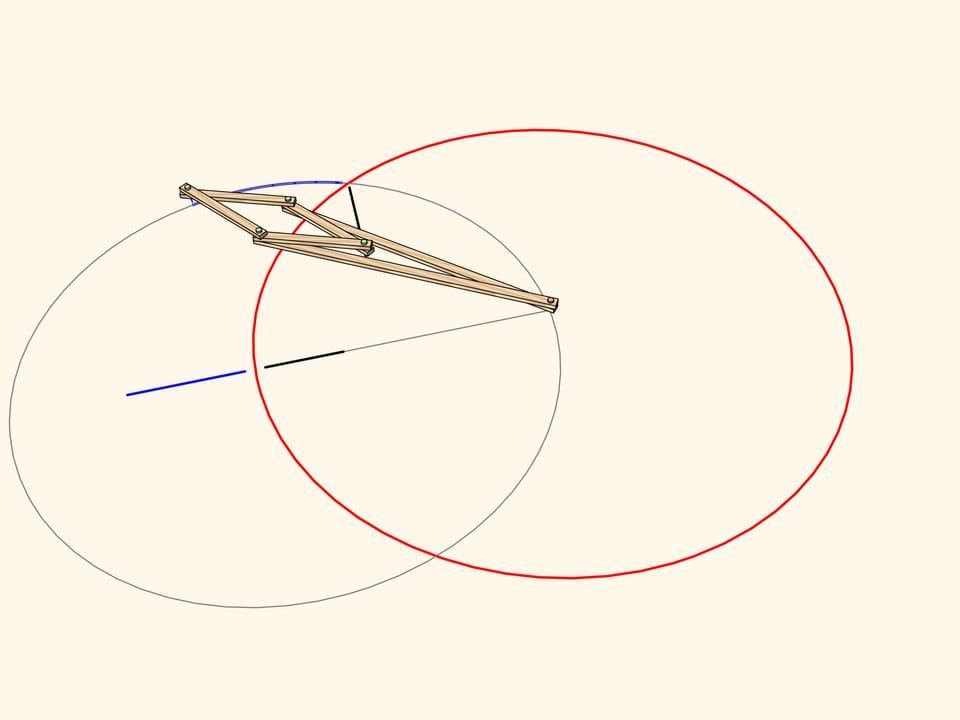
A circle not passing through the center of inversion and not intersecting the inversion circle maps again to a circle.
Inversion changes orientation. Similar transformations in mathematics are called anti-conformal (conformal are those that preserve both angles and their orientation).
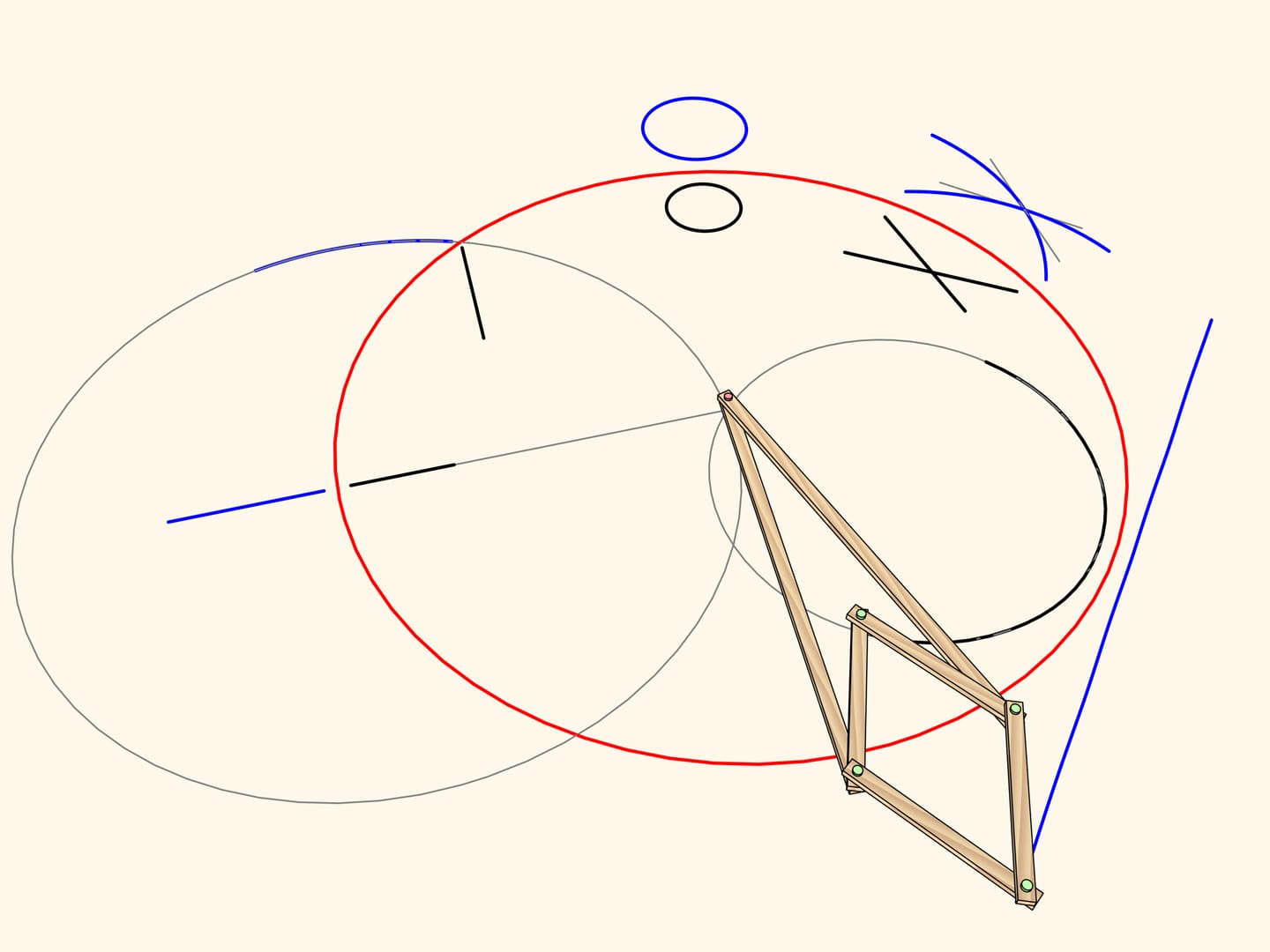
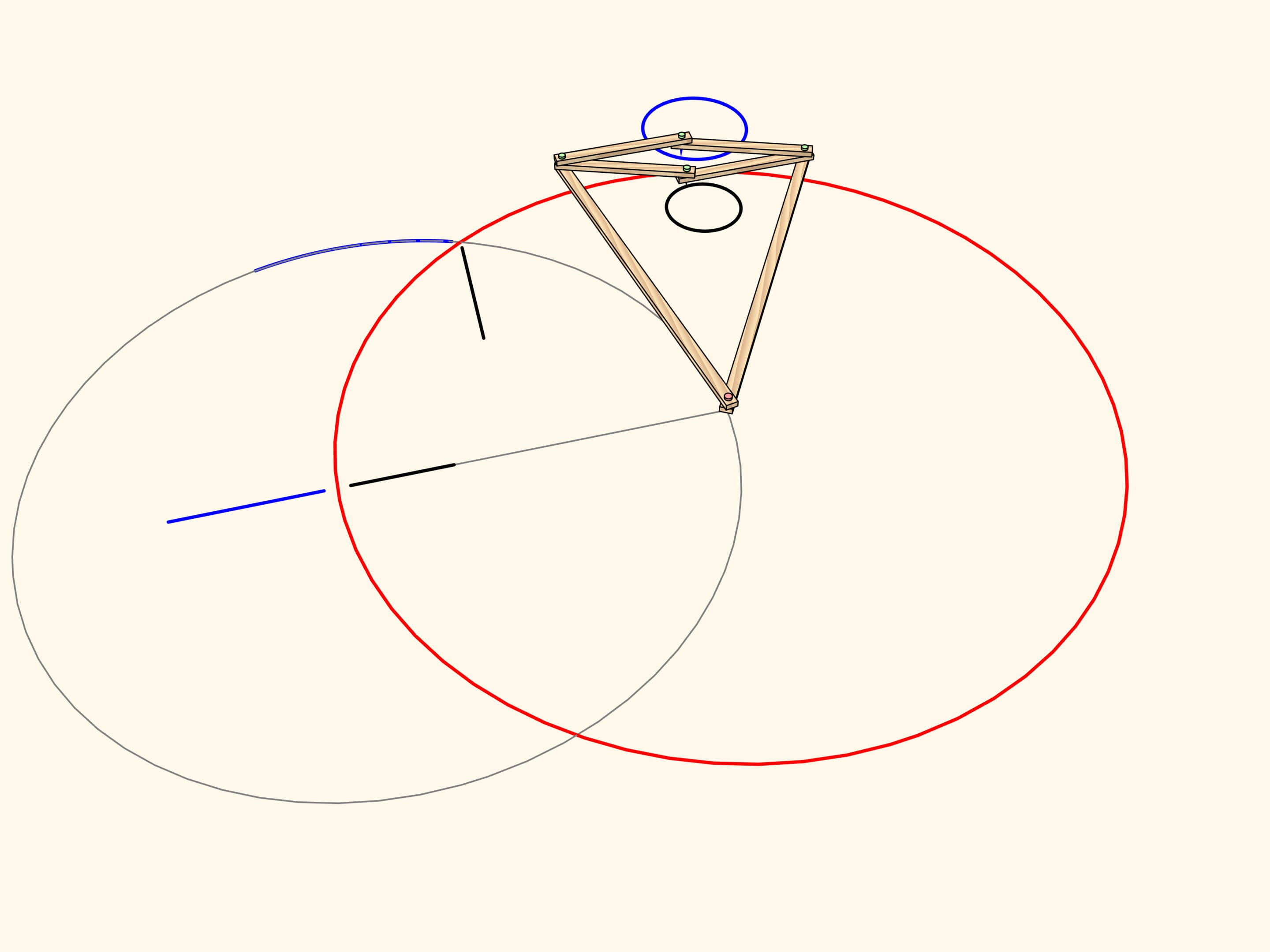
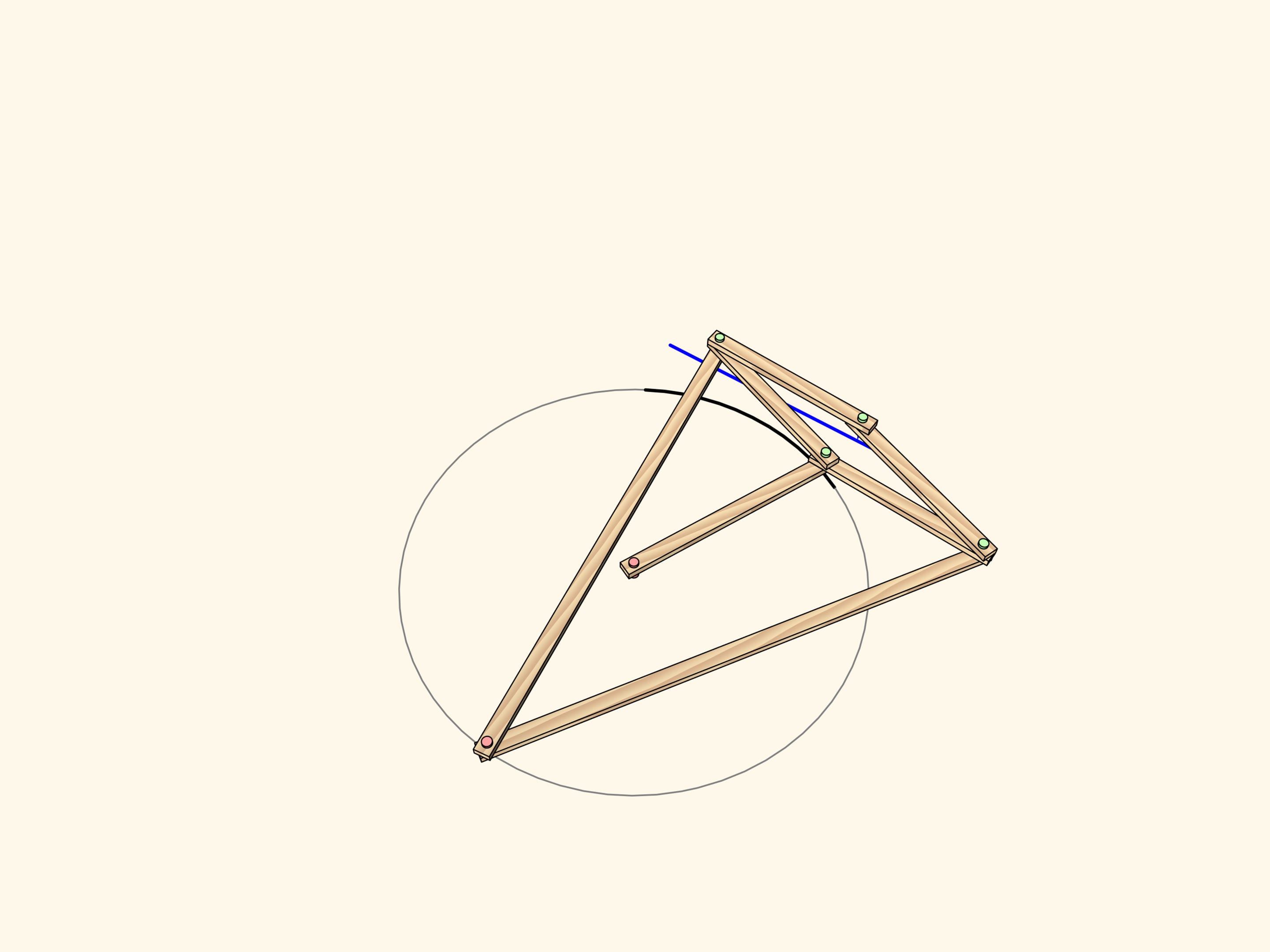
An arc of a circe passing through the center of inversion maps to… a strict straight-line segment!
Exactly this property has been used to construct the straight-line linkage. Add a fixed hinge in the center of the circle and an edge of radius length so that the leading hinge follows the circular path. Thus, the driven hinge will always follow a straight-line segment. This kind of mechanisms are often called inversors.
In 1864 in a private letter an engineer of the French army Charles Nicolas Peauncellier (1823—1913) announced his construction of an inversor. However, he didn't mention any details. In 1868 a student of P. L. Tchebyshev, Lipman Lipkin (1846—1876), invents an inversor. His detailed paper was published in 1870 and only in 1873 Peauncellier publishes his one describing exactly the same mechanisms and citing Lipkin.
Afterwards, there were other linkages constructed based on other mathematical ideas. However, the inversor is notable for its beauty, good mechanical properties and is widely used in techniques.