What is the net of a polyhedron? It is simply a sheet of cardboard whose folding gives the polyhedron. – May you answer. This is true, but there’s more. The concept of the net of a polyhedron contains something more than just a sheet of cardboard.
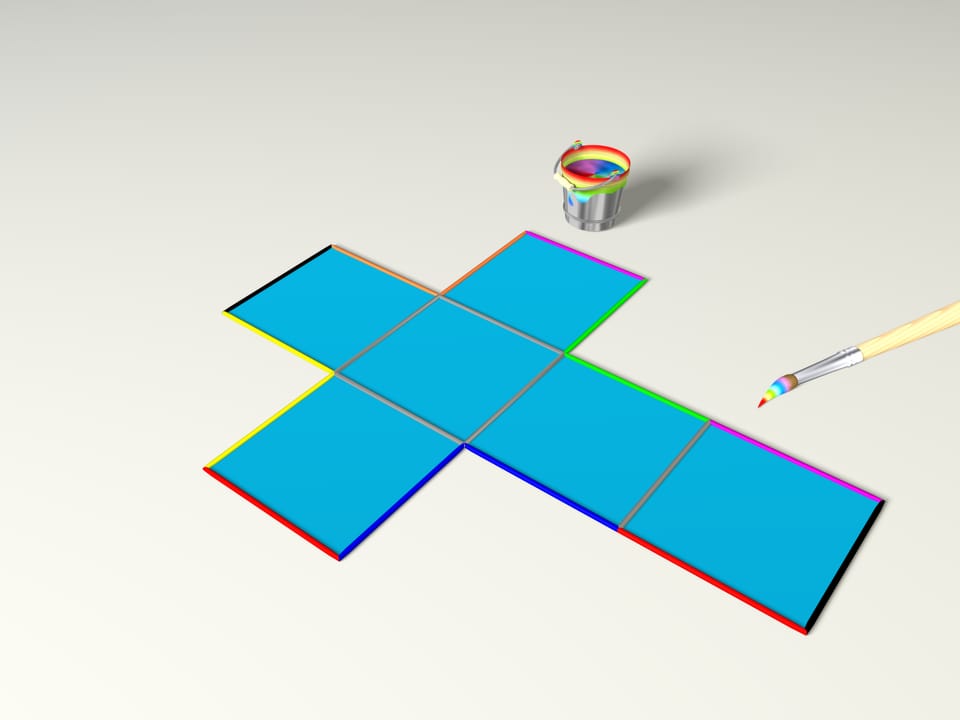
Which polyhedron can be achieved by folding the familiar Latin cross? The cube, of course. For this we should colour the edges, as our magic brush did (the edges of the same colour are glued to each other in the polyhedron).
However, it would be better to colour with different colours not the edges, but each pair of points. This should correspond to giving, as it is said in mathematics, the conditions of edges’ gluing.
After that the conditions of edges’ gluing are given, the edges located inside the sheet of cardboard are uniquely defined, according to a theorem by A.D. Aleksandrov.
So from the Latin cross, you can get a cube.
But it happens that if the conditions are given otherwise, you can get something but a cube!
Our magic brush has coloured the edges here’s how. A final stroke of his and we already know how to define the edges within the piece of cardboard. Then we will construct a polyhedron, following the conditions of gluing just designed: we get a pyramid!
Not long ago it was shown that giving different conditions of gluing the edges of the Latin cross, you can get 5 different types of convex polyhedra.
So, as we have seen, the concept of net of a polyhedron dos not consist just of a sheet of cardboard, but also of the gluing conditions of its edges. If these conditions are not defined, then from the same piece of cardboard you may get different convex polyhedra.